ローレンツブーストは虚数角の座標回転

こちらの記事の最後で「ローレンツ・ブーストは虚数角の座標回転を表す」と書きました。
（ローレンツ変換とローレンツ・ブーストにはこちらの記事に書いたような違いがあります。一般にはローレンツ・ブーストのことをローレンツ変換と呼ぶことも多いです）

ローレンツ・ブーストとは速度の異なる慣性系への座標変換で、特殊相対性理論の柱となります。
具体的には次式です（x方向ブーストの場合。導出はこちら）。
$$
\left(\begin{array}{c}
ct’ \\ x’ \\ y’ \\ z’
\end{array}\right)
=
\begin{pmatrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}
\left(\begin{array}{c}
ct \\ x \\ y \\ z
\end{array}\right) \tag{1}$$
この記事では、ローレンツ・ブーストを虚数角の座標回転とみなすことについて
・みなせるための条件
・みなせる理由の説明
を順に説明します。

（スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします）

虚数角の座標回転とみなせるための条件は？

ローレンツ・ブーストを虚数角の回転だとみなすには、ひとつ前提条件があります。
それは、
特殊相対論でおなじみの x-ct グラフ（ミンコフスキー図）で考えるのではなく、x-ict グラフで考える必要がある
ということです。

もしもx-ct グラフで考えると、ご存知のとおり x-ct グラフはローレンツ・ブーストによって x 軸と ct 軸が斜交するように変形するので、回転の関係にはなりません（下図）。

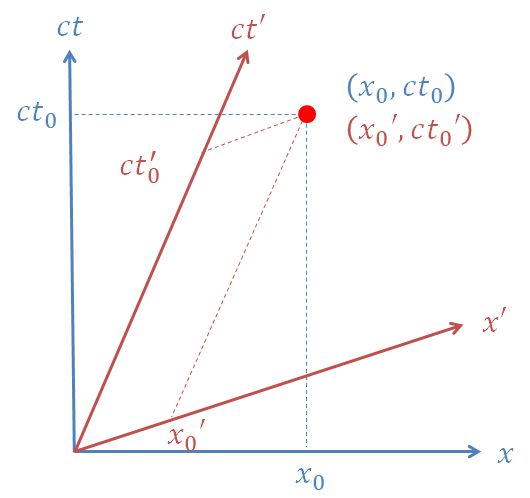
一方、横軸を $x$, 縦軸を $ict$ とするグラフで考えれば、ローレンツ・ブーストは虚数角の回転とみなすことができます（下図）。

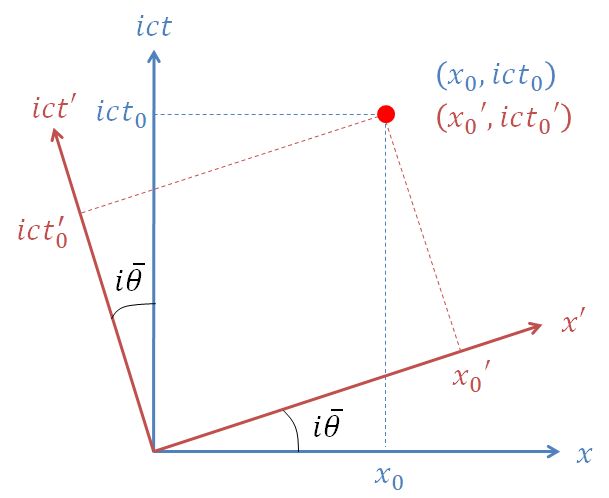横軸を $x$, 縦軸を $ict$ とするグラフで考えれば、ローレンツ・ブーストは虚数角の回転とみなせる理由をこれから説明します。

■虚数角の座標回転とみなせる理由は？

【命題】
ローレンツ・ブーストは、$\gamma = \cos{i \bar{\theta}}$ （$\bar{\theta}$: 実数）とおくと、
$x-ict$ 平面で $i\bar{\theta}$ 回転する変換だと解釈できる。

図は1つ上の図をご覧ください。
話をシンプルにするため、空間軸は $x$ 軸だけとして考えます。

■ ローレンツ・ブーストの式から出発、回転を表す式へと変形していく

まず、ローレンツ・ブーストは次のように書けます。(1)の空間軸を $x$ 軸だけにしたものです。
$$
\left(\begin{array}{c}
ct’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \gamma & -\gamma \beta \\ -\gamma \beta & \gamma\end{pmatrix}
\left(\begin{array}{c}
ct \\ x
\end{array}\right) \tag{2}$$方針としては、この式を変形して、なるべく普通の空間座標における回転を表す式
$$
\left(\begin{array}{c}
y’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{pmatrix}
\left(\begin{array}{c}
y \\ x
\end{array}\right) \tag{3}$$の形に近づけていきます（(3)の両辺の上が $y$ 成分、下が $x$ 成分になっている理由は、(2)で縦軸である $ct$ 軸の座標を上に書いていることに対応させるためです）。

■ 何から手をつけるか

x-y 座標系での回転の不変量は $x^2 + y^2$ （原点からの空間的な距離）です。
一方、x-ct 座標系でのローレンツ・ブーストの不変量は $-(ct)^2 + x^2$ です。
一応確認してみると
$$-(ct’)^2 + (x’)^2 = -(\gamma ct – \gamma \beta x)^2 + (-\gamma \beta ct + \gamma x)^2 = \cdots = (ct)^2 – x^2$$となり、たしかに不変量になっています。$(ct)^2 + x^2$ だと不変量にはなりません。

つまり、x-y座標系の回転とx-ct座標系のローレンツ・ブーストでは不変量が異なるのです。

なので、まずは x-ct 座標系のローレンツ・ブーストにおける不変量を、x-y 座標系と同じ形の式になるようにします。

■ 不変量の定義式を空間における距離の定義式の形にする

x-ct 座標系のローレンツ・ブーストにおける不変量を、x-y座標系における不変量（距離）の定義式と同じ形にするにはどうすればよいでしょうか。

それは、x-ct グラフから x-ict グラフに変更することです。

どういうことかを図に示します。

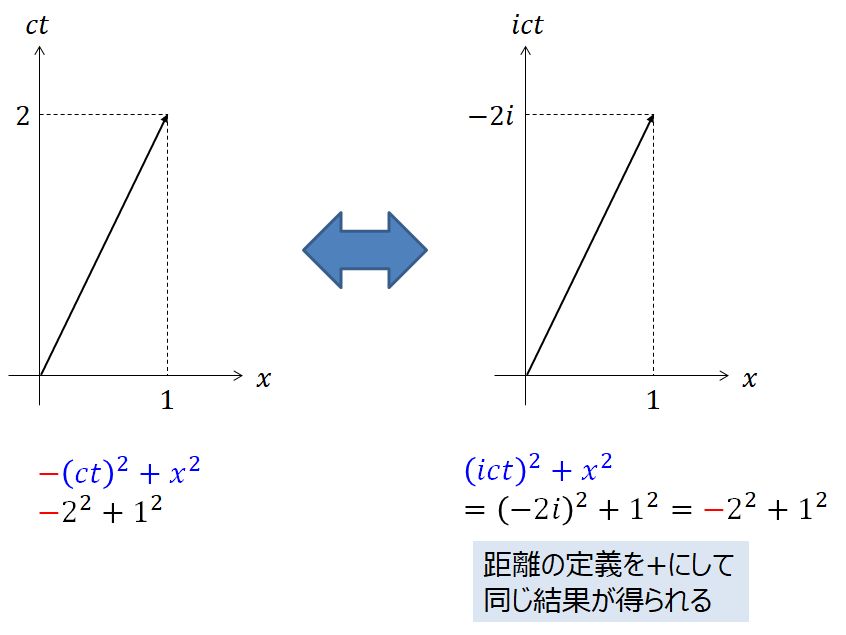
左が x-ct グラフ（ミンコフスキー図）、右が x-ictグラフです。これらは等価です。

左のグラフの $ct = 2$ という座標は、右のグラフの $ict = -2i$ と等価です（$(-2i)(ict)=2ct$ より）。

左のグラフの不変量は $-(ct)^2+x^2$ なのに対して右のグラフの不変量は $(ict)^2 + x^2$ です。
等価性を維持したまま、x-yグラフと同じ計算式で計算することができるようになりました(^^)。

では、ローレンツ・ブーストの式 (1) の第1成分を $ct$ から $ict$ に変更してみましょう。
$$
\left(\begin{array}{c}
ict’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \gamma & -i\gamma \beta \\ i\gamma \beta & \gamma\end{pmatrix}
\left(\begin{array}{c}
ict \\ x
\end{array}\right) \tag{4}$$これで x-y グラフと同じ計算式で不変量が計算できるはずです。
念のため確認しておきましょう。
$$(ict’)^2 + (x’)^2 = (i \gamma ct – i \gamma \beta x)^2 + (-\gamma \beta ct + \gamma x)^2 = \cdots = (ict)^2 + x^2 \tag{5}$$OKですね。不変量を $-(ct^2) + x^2$ から $(ict)^2 + x^2$ に変えることができました。

■ 回転の形で表す

(2)と(4)を並べてみます。
$$
\left(\begin{array}{c}
y’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{pmatrix}
\left(\begin{array}{c}
y \\ x
\end{array}\right) \tag{2}$$$$
\left(\begin{array}{c}
ict’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \gamma & -i\gamma \beta \\ i\gamma \beta & \gamma\end{pmatrix}
\left(\begin{array}{c}
ict \\ x
\end{array}\right) \tag{4}$$そっくりですね。あとは(4)を(2)の形に書き換えられることを示せればOKです。

まず変換行列の左上の成分に注目しましょう。

(2) の $\cos{\theta}$ に対応するのは(4)の $\gamma$ ですね。単純に考えれば
$$\gamma = \cos{\theta} \tag{5}$$とおきたいところですが、$\left| \cos{\theta} \right| \le 1$ なのに対して $\gamma$ は $\gamma \ge 1$ なのでそのまま置き換えるわけにはいきません。

ここでちょっとひらめきが必要なのですが、もしも $\theta$ が虚数で $\theta = i \bar{\theta}$ ($\bar{\theta}$ は実数) とすると(5)はどうなるでしょうか？

双曲線関数の公式 $\cos{ix} = \cosh{x}$ を使うと
$$\gamma = \cos{i \bar{\theta}} = \cosh{\bar{\theta}} \tag{6}$$となります（双曲線関数についてはこちらにまとめてあります）。

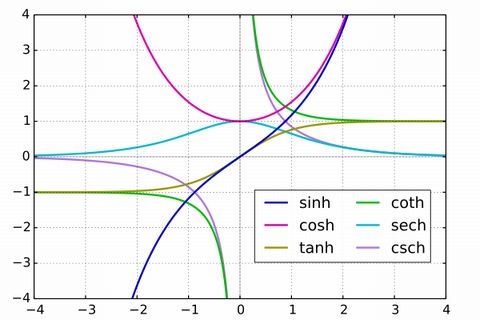
$\cosh{\bar{\theta}}$ であれば、下図のとおり $\cosh{\bar{\theta}} \ge 1$ なので $\gamma$の値をカバーできます。
任意の $\gamma$ の値に対して対応する $\bar{\theta}$ が2つ存在することもわかります。

では次。変換行列の左下の成分に注目しましょう。

(2)の $\sin{\theta}$ に対応するのは(4)の $i\gamma \beta$ ですね。
ここで
\begin{eqnarray}(\gamma \beta)^2 &=& \frac{\beta^2}{1-\beta^2} = \frac{1 – (1 -\beta^2)}{1-\beta^2} \\
&=& \gamma^2 – 1 = \cosh^2{\bar{\theta}} -1 = \sinh^2{\bar{\theta}}\end{eqnarray}より
$$\gamma \beta = \pm \sinh{\bar{\theta}}$$ここで左辺の$\gamma \beta$ は任意の実数値を取り得ますが、$\sinh{\bar{\theta}}$ のグラフが上図のようであることを考えると、$+\sinh{\bar{\theta}}$ ですべて対応できます。そこで、与えられた $\gamma, \beta$ に対して
$$\gamma \beta = \sinh{\bar{\theta}}$$とおくことにします。すると、さきほど $\bar{\theta} \ge 0$の符号によって、2つ存在しえるとしていた $\cosh{\bar{\theta}}$ の $\bar{\theta}$ も1つに決まることになります。

よって再掲すると
$$
\left(\begin{array}{c}
y’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta}\end{pmatrix}
\left(\begin{array}{c}
y \\ x
\end{array}\right) \tag{2}$$$$
\left(\begin{array}{c}
ict’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \gamma & -i\gamma \beta \\ i\gamma \beta & \gamma\end{pmatrix}
\left(\begin{array}{c}
ict \\ x
\end{array}\right) \tag{4}$$の(4)は
$$
\left(\begin{array}{c}
ict’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \cosh{\bar{\theta}} & -i \sinh{\bar{\theta}} \\ i \sinh{\bar{\theta}} & \cosh{\bar{\theta}}\end{pmatrix}
\left(\begin{array}{c}
ict \\ x
\end{array}\right) \tag{7}$$と書き換えられることがわかりました。

最終目標は(2)の形であって(7)の形ではありません。

そこで再び双曲線関数の公式を使います。
$$\cos{ix} = \cosh{x}, \ \ \sin{ix} = i \sinh{x}$$$$\cosh{ix} = \cos{x}, \ \ \sinh{ix} = i \sin{x}$$ を使うと(7)は
$$
\left(\begin{array}{c}
ict’ \\ x’
\end{array}\right)
=
\begin{pmatrix} \cos{i\bar{\theta}} & -\sin{i\bar{\theta}} \\ \sin{i \bar{\theta}} & \cos{i\bar{\theta}}\end{pmatrix}
\left(\begin{array}{c}
ict \\ x
\end{array}\right)$$となります。

これで命題