【相対論】 「時空の距離」の定義　バリエーション一覧

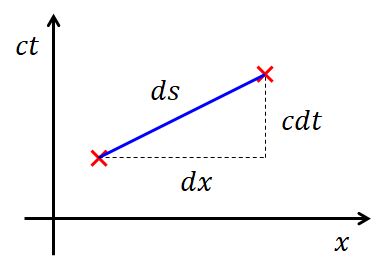
特殊相対性理論では時間と空間が融合した「時空」を考えます。

その際、（時空を図で表した）ミンコフスキー図上の2点(2事象)間の距離の定義方法が本によっていろんな流儀があります。
どんなバリエーションがあるのか、手元にある本を元にまとめてみました。

大別すると、距離の2乗 (\(ds^2\)) の符号の取り方によって2種類に分けられるかと思います。
・タイプA: ２つの事象が timelike (時間的。物理的) に隔てられている場合に正と定義するタイプ
・タイプB: 2つの事象が spacelike (空間的) に隔てられている場合に正と定義するタイプ
（「timelike」「spacelike」の意味は、平たく言えば、2つの事象を結ぶ直線の傾きが ct 軸寄りならtimelike、空間軸(x軸など)寄りならspacelikeです）

また、\(ds\) の呼び方も本によっていろいろです。

タイプ A 系 (timelikeを \(ds^2 \ge 0\) とする）

・【 タイプ A-1 】 \(ds^2 = (c dt)^2 – (dx^2 + dy^2 + dz^2)\)
　(例)
　・「MaRu‐WaKaRi 場の量子論」David McMahon 　「世界間隔」
　・「場の量子論: 不変性と自由場を中心にして」 坂本眞人　「距離」
　・「新版 演習 場の量子論」 柏太郎　「長さ」

・【 タイプ A-2 】 \(d \tau ^2 = (c dt)^2 – (dx^2 + dy^2 + dz^2)\)
　【 タイプ A-1 】で左辺の \(s\) を \(\tau\) にして「固有時」と呼ぶタイプ。
　(例)
　・「趣味で相対論」　広江克彦　「固有時」
　・「相対論入門」 中村純　「固有時」

・【 タイプ A-3 】 \(-ds^2 = -(c dt)^2 + (dx^2 + dy^2 + dz^2)\)
　【 タイプ A-1 】の両辺の符号を反転するタイプ。
　(例)
　・「初級講座弦理論 基礎編」Barton Zwiebach　「不変距離 (invariant interval)」
　・「string theory DeMYSTiFieD」 David McMahon

タイプ B 系 (spacelikeを \(ds^2 \ge 0\) とする）

・【 タイプ B-1 】 \(ds^2 = – (c dt)^2 + (dx^2 + dy^2 + dz^2)\)
　右辺の符号が【 タイプ A 】とは逆になるタイプ。
　(例)
　・「重力」ハートル　「線素」
　・「あきらめない一般相対論」　富岡竜太　「世界間隔」
　・一般相対性理論を一歩一歩数式で理解する」石井 俊全　「「ミンコフスキー距離」

・【 タイプ B-2 】 \(ds^2 = (dx^2 + dy^2 + dz^2) – (c dt)^2\)
　【 タイプ B-1 】で時間項 \(-(cdt)^2\) と空間項 \((dx^2 + dy^2 + dz^2)\) の順序を入れ替えたタイプ。
　(例)
　・「高校数学でわかる相対性理論」　竹内淳　「世界距離」　
　・「相対性理論の考え方」 砂川重信　「不変距離」
　・「物理入門コース9 相対性理論」　中野董夫　「世界距離」

好み、思想の違い

勝手な想像ですが、タイプA とタイプB の思想の違いはこんな感じでしょうか？↓
・タイプA:
　　点粒子が物理的な運動（光速を超えない運動）をした時の距離が正になるように定義した
・タイプB:
　　非相対論的な空間の距離が正であることに合わせて spacelike な距離が正になるように定義した

個人的には、本によって「この本はどのタイプだっけ？」と毎度確認するのが面倒なので、どれかに統一する動きがあるといいなーと思います (^^;