「地球の質量は?」と聞かれて、…
運動エネルギー (1/2) mv^2 の導出

運動エネルギー \(T\) が
$$T=\frac{1}{2}mv^2 \tag{1}$$と表されることは暗記していると思いますが、この導き方って覚えてますでしょうか?
いろんな方法があると思いますが、そのうちの1つをご紹介します。
(スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします)
■ 歴史
その前にちょっと運動エネルギーにまつわる歴史をご紹介します(放送大学「初歩からの物理(2016)」第5回 より)。
歴史的には、ニュートンとライプニッツが運動の基本量をめぐって議論していたそうです。
・ニュートン(1642-1727年):運動の基本量は「運動量」 \(m \vec{v}\) だ!
・ライプニッツ(1646-1716年):運動の基本量は「活力」\(mv^2\) だ!
ライプニッツの「活力」は今では \(\frac{1}{2}\)いう係数がついて運動エネルギーと呼ばれていますね。
運動量と運動エネルギー、今ではどちらが基本量ということはないと思いますので、どちらも正しいと言ってよさそうです。
運動量はベクトル、活力は \(\vec{v}\) を2乗してますのでスカラーという特徴がありますね。
「活力」を「エネルギー」と呼ぶことを提案したのは、ライプニッツから200年近く後のトマス・ヤング(1773-1829年)だそうです。
■ \(T = \frac{1}{2} m v^2\) の導出
では \(T = \frac{1}{2} m v^2\) を導出してみましょう。
下図のように、質点の軌道上に2点A,B を取って、その間を微小な長さ \(ds\) に分割します。
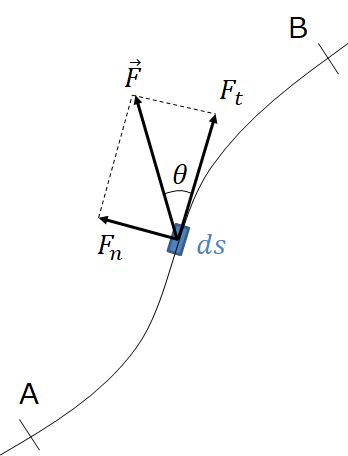
質点に働く力を \(\vec{F}\)、そのうち粒子の軌道方向成分を \(F_t\)、質点の速さを \(|\vec{v}| = v\) とします。
軌道に沿った方向のニュートンの運動方程式は
$$F_t = m \frac{dv}{dt}$$両辺に \(ds\) をかけると
$$F_t ds= m\frac{dv}{dt}ds$$ここで \(v = ds/dt\) より \(ds = v \ dt\) を代入すると
$$F_t ds = m v \frac{dv}{dt} dt = mv \ dv$$両辺をAからBまで積分すると
$$\int_A^B {F_t ds} = m \int_A^B {v \ dv}$$左辺の被積分関数は、\(ds\) の微小変位のベクトルを \(d\vec{r}\) で表すと \(\vec{F}\cdot d\vec{r}\) とおけます。
さらに右辺の積分も実行すると
$$\int_A^B {\vec{F}\cdot d\vec{r}}= \frac{1}{2}m {v_B}^2 – \frac{1}{2}m {v_A}^2$$
左辺を、力がAからBまでの間になした「仕事」と定義します。
右辺は、\(F_t\) による加速または減速の効果が \(\frac{1}{2} mv^2\) という量の増減で表されることを示しています。
この \(\frac{1}{2} mv^2\) のことを質点の運動エネルギーと定義するのでした。
以上を振り返ると、ライプニッツの「活力」\(mv^2\) が運動エネルギーと呼ばれるようになるにあたって 1/2 がついたのは、運動量の大きさ \(mv\) を \(v\) で積分したことによることがわかりますね。
次回は本記事の結果から力学的エネルギー保存則を導きます。
参考:
・放送大学「初歩からの物理」第5回
・力学 (物理テキストシリーズ 1)

13

