X軸、Y軸、Z軸が直線で直交し…
双曲線関数(cosh, sinh, tanh)の重要事項まとめ
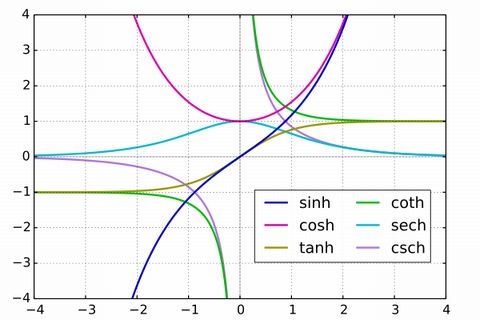
大学の物理では、高校数学に出て来る三角関数 \(\sin{x}, \cos{x}, \tan{x}\) と見た目が似たような、双曲線関数 \(\sinh{x}, \cosh{x}, \tanh{x}\) というのが出てきます。
この双曲線関数の重要事項を、三角関数と比較しながらまとめておきます。
(スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします)
■ 名前の由来
三角関数の組み合わせ \((a\cos{\theta}, a\sin{\theta})\) は円 \(x^2 + y^2 = a^2\) 上の点の座標を媒介変数表示したものでした。
一方、双曲線関数の組み合わせ \((a\cosh{\theta}, a\sinh{\theta})\) は双曲線 \(x^2 – y^2 = a^2\) 上の点の座標を媒介変数表示したものです(「双曲線関数」と呼ばれる理由はこれ)。
■ 読み方
・きちんと読む場合・・・「ハイパボリック・コサイン」「ハイパボリック・サイン」「ハイパボリック・タンジェント」
・略称・・・「コッシュ」「シンチ」「タンチ」
■ 基本的な関係式
$$\cosh{x} = \frac{e^x+e^{-x}}{2}, \ \ \sinh{x} = \frac{e^x-e^{-x}}{2}, \ \ \tanh{x} = \frac{\sinh{x}}{\cosh{x}}$$$$\cosh^2{x} – \sinh^2{x} = 1$$なお三角関数は(オイラーの公式 \(e^{ix} = \cos{x} + i \sin{x}\) より)
$$\cos{x} = \frac{e^{ix}+e^{-ix}}{2}, \ \ \sin{x} = \frac{e^{ix}-e^{-ix}}{2i}, \ \ \tan{x} = \frac{\sin{x}}{\cos{x}}$$$$\cos^2{x} + \sin^2{x} = 1$$
■ 加法定理
$$\sinh(x_1 + x_2) = \sinh{x_1} \cosh{x_2} + \cosh{x_1}\sinh{x_2}$$$$\sinh{2x} = 2 \sinh{x}\cosh{x}$$$$\cosh(x_1 + x_2) = \cosh{x_1} \cosh{x_2} + \sinh{x_1}\sinh{x_2}$$$$\cosh{2x} = \cosh^2{x} + \sinh^2{x} = 2\cosh^2{x}-1 = 2\sinh^2{x} + 1$$なお三角関数は・・・
$$\sin(x_1 + x_2) = \sin{x_1} \cos{x_2} + \cos{x_1}\sin{x_2}$$$$\sin{2x} = 2 \sin{x}\cos{x}$$$$\cos(x_1 + x_2) = \cos{x_1} \cos{x_2} – \sin{x_1}\sin{x_2}$$$$\cos{2x} = \cos^2{x} – \sin^2{x} = 2\cos^2{x}-1 = 1 – 2\sin^2{x}$$
■ 微分
$$(\cosh{x})’ = \sinh{x}, \ \ (\sinh{x})’ = \cosh{x}$$なお三角関数は・・・
$$(\cos{x})’ = -\sinh{x}, \ \ (\sin{x})’ = \cos{x}$$
■ 双曲線関数と三角関数との関係式
$$\cos{ix} = \cosh{x}, \ \ \sin{ix} = i \sinh{x}$$$$\cosh{ix} = \cos{x}, \ \ \sinh{ix} = i \sin{x}$$変数を複素数にまで拡張すれば、双曲線関数と三角関数は密接に関連していることがわかります。
■ 使う場面の例
・ラプラス方程式、拡散方程式の解
・ローレンツ変換の解釈
・懸垂線の式
・量子力学のトンネル効果
補足事項が出てきたら追記していきます。
参考:
・https://ameblo.jp/kazuaha63/entry-11308245633.html
・道具としての微分方程式―「みようみまね」で使ってみよう (ブルーバックス)

・物理のための数学 (物理入門コース 新装版)

・高校数学でわかる相対性理論 (ブルーバックス)

0

