速度ベクトルの大きさはスカラーか？

【問題】速度ベクトルの大きさはスカラーか？

「速度ベクトルの大きさ（＝速さ）はスカラーである」という説明を聞くことがあります。

一方、「スカラーとは座標変換しても値が変わらない量である」という定義も見ます。

これらって矛盾してないでしょうか？

どういうことかというと、例えばある座標系 S から見て速度が $\vec{v}$ の物体があったとします。
ここで S に対して物体と同じ速度 $\vec{v}$ で動く座標系 S’ から見ると、速度の大きさはゼロになりますよね。

座標変換して値が変わってしまってます。
なので「速度の大きさはスカラーではないのでは？」という気もします。

どう考えれば矛盾がなくなるでしょうか？

【結論】4元速度 + ローレンツ変換で考えれば、速度の大きさは座標変換に対して不変になる

上記の混乱は、「スカラー」「変換」「速度」をきちんと定義していないことが原因です。

速度を4元速度、座標変換をローレンツ変換で考えれば、速度の大きさ（の2乗）は S から見ても S’ から見ても $-c^2$ で値は変わりません。（導出や意味についてはのちほど）

なので、スカラーを「座標変換しても値が変わらない量」と定義するなら、4元速度の大きさはローレンツ変換に対してスカラーです。

一方、4元速度ではなく時間成分を持たない古典的速度（＝高校生で習う3次元の速度）で考えたり、ローレンツ変換ではなくガリレイ変換で考えたりした場合は、問題文にあるとおり、速度の大きさは座標変換に対して不変ではありません。

また、スカラーの定義を座標変換云々は抜きにして単に「向きを持たず大きさだけを持つ量」と定義するなら、古典的速度で考えても速度の大きさはスカラーです。

4元速度とは？

4元速度とは、特殊相対論で出てくる速度です。
古典的速度との大きな違いは、空間方向の3成分に加えて時間方向にも成分を1つ持っているので合計4成分あるということです。

古典的速度 $\vec{v}=(v_x, v_y, v_z)$ を4元速度で表すと下記のようになります。
$$\vec{u}=\left(\color{red}{\frac{c}{\sqrt{1-\frac{|\vec{v}|^2}{c^2}}}}, \frac{v_x}{\color{red}{\sqrt{1-\frac{|\vec{v}|^2}{c^2}}}}, \frac{v_y}{\color{red}{\sqrt{1-\frac{|\vec{v}|^2}{c^2}}}}, \frac{v_z}{\color{red}{\sqrt{1-\frac{|\vec{v}|^2}{c^2}}}}\right) \tag{1}$$(なぜか成分の上に少し空白が空いてしまってます;;)

赤字の部分が4元速度固有の部分です。

問題文の場合、S’ から見た物体の古典的速度は $(v_x, v_y, v_z) = (0,0,0)$ になるわけですが、4元速度としては $(c, 0, 0, 0)$ となり、時間成分が最大の $c$ になります。

S と S’ で速度の大きさが一致することの確認

4元速度などの4元ベクトルの大きさは、古典的ベクトルとは違って下記の式で定義されています。
$\vec{v}=(v_t, v_x, v_y, v_z)$ とすると $|\vec{v}|^2 = \color{red}{-}{v_t}^2 + {v_x}^2 + {v_y}^2 + {v_z}^2$
時間成分だけ2乗の符号がマイナスになることに注意してください。

なので、 S’ から見た物体の4元速度の大きさ（の2乗）は、
$|\vec{v}|^2 = -c^2 + 0^2 + 0^2 + 0^2 = -c^2$
となります。

これが S から見た物体の速度の大きさに一致するか確認してみます。

S から見た物体の古典的速度を $(v_x, v_y, v_z) = (v, 0, 0)$ とすると、その4元速度は (1) に代入して $\left(\frac{c}{\sqrt{1-\frac{|v|^2}{c^2}}}, \frac{v}{\sqrt{1-\frac{|v|^2}{c^2}}}, 0, 0\right)$ です。

この大きさ（の2乗）を S’ のときと同様に計算すると、めでたく $-c^2$ となり、S’ から見たものと一致します（計算過程は省略）。

(おまけ) 4元速度のイメージ

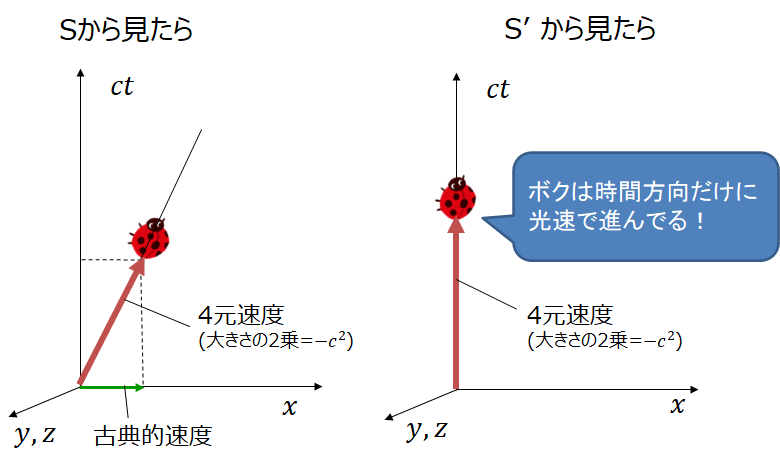
上記のように、4元速度（の2乗）は誰から見ても $-c^2$ という大きさを持っています。

新幹線に乗った人が見ても、月から見ても。

そして観測対象の物体自身から見ても。

観測対象の物体自身にしてみれば、自分は自分自身に対して常に静止しているので、空間方向の速度成分はゼロですが、時間方向に速度を持っているというのがミソですね。

だれもが時間方向に光速で移動していると捉えることができます。

年を取るっていうのは、相対論的には時空の中を時間軸方向に光速で移動することなんですね。

そしてその観測対象の物体に対して空間的な速度を持っている人から見ると、物体の時間方向への移動の一部が空間成分の速度として観測されてるんですね。

3