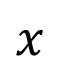【相対論】計量は基底の内積データベース！

■ 疑問

相対性理論で「計量 $g_{\mu\nu}$」という記号が出てきます。

例えば、特殊相対論で扱うミンコフスキー空間の計量は
$$g_{\mu\nu}=\left(
\begin{array}{cccc}
-1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{array}
\right)$$ですね。対応する英語は「metric」です。

計量を始めて見たとき私は

「動詞なの？名詞なの？」
「何を計るの？」
「どうしてこんな成分になるの？」

など理解できないことがたくさんありました。

■ 計量は「基底の内積データベース」

今の私なら、「計量って何？」と聞かれたらズバリ

「計量は基底の内積データベースです！」

と答えます。

先の初心者時代の私の疑問に解答するなら、

「動詞なの？名詞なの？」⇒名詞です
「何を計るの？」⇒いろんなものを測ります
「どうしてこんな成分になるの？」⇒各成分に対応する基底の内積を計算すると、そういう値になるからです

となります。

「計量は基底の内積データベース」とはどういうことでしょうか？
それは、計量の定義式を見れば明らかです。
$$g_{\mu\nu}=\left(
\begin{array}{cccc}
\textbf{e}_1\cdot\textbf{e}_1 & \textbf{e}_1\cdot\textbf{e}_2 & \ldots & \textbf{e}_1\cdot\textbf{e}_n \\
\textbf{e}_2\cdot\textbf{e}_1 & \textbf{e}_2\cdot\textbf{e}_2 & \ldots & \textbf{e}_2\cdot\textbf{e}_n \\
\vdots & \vdots & \ddots & \vdots \\
\textbf{e}_n\cdot\textbf{e}_1 & \textbf{e}_n\cdot\textbf{e}_2 & \ldots & \textbf{e}_n\cdot\textbf{e}_n \\
\end{array}
\right)$$ご覧のとおり全基底の内積の組み合わせを網羅しています。
なのでデータベースと呼びました。

全空間に対して一様に正規直交基底が効いている場合は、わざわざ計量なんてデータベースを持ち出す必要はないかもしれません。
しかし一般相対性理論では曲がった時空も対象とするので、基底どうしの内積が座標の関数になったりします。そこで基底の内積をデータベースとして持っておくことで計算しやすくしようというわけです。

なお、ご覧のとおり計量は対称行列で、しかも内積は左右を入れ替えても同じ値なので、上三角成分だけで情報量としては十分です。

■ 基底の内積でいろんな量が計算できる

ではなぜ基底の内積データベースが「計量」と呼ばれるのでしょうか？
それは、いろんな量が基底の内積を使って計算できるからだと思います。

例えば、n 次元空間における2点間の距離 $d$ は、2点間を結ぶベクトルを $\boldsymbol{V}=V^1\textbf{e}_1+V^2\textbf{e}_2+\cdots+V^n\textbf{e}_n$とすると次のように書けます。\begin{eqnarray}
d &\equiv& \boldsymbol{V}\cdot\boldsymbol{V}\\
&=& (V^1\textbf{e}_1+V^2\textbf{e}_2+\cdots+V^n\textbf{e}_n)\cdot(V^1\textbf{e}_1+V^2\textbf{e}_2+\cdots+V^n\textbf{e}_n)\\
&=& (V^1)^2\textbf{e}_1\cdot\textbf{e}_1+V^1V^2\textbf{e}_1\cdot\textbf{e}_2+\cdots+V^1V^n\textbf{e}_1\cdot\textbf{e}_n\\
& &+V^2V^1\textbf{e}_2\cdot\textbf{e}_1+(V^2)^2\textbf{e}_2\cdot\textbf{e}_2+\cdots+V^2V^n\textbf{e}_2\cdot\textbf{e}_n\\
& &\vdots\\
& &+V^nV^1\textbf{e}_n\cdot\textbf{e}_1+V^nV^2\textbf{e}_n\cdot\textbf{e}_2+\cdots+(V^n)^2\textbf{e}_n\cdot\textbf{e}_n\\
&=& (V^1)^2g_{11}+V^1V^2g_{12}+\cdots+V^1V^ng_{1n}\\
& &+V^2V^1g_{21}+(V^2)^2g_{22}+\cdots+V^2V^ng_{2n}\\
& &\vdots\\
& &+V^nV^1g_{n1}+V^nV^2g_{n2}+\cdots+(V^n)^2g_{nn}\\
(&=&\displaystyle \sum_{i,j}g_{ij}V^iV^j)\tag{1}
\end{eqnarray}基底の内積をフル活用してますね。

■ 高校数学との違い

高校数学で習った内積の公式は2つのベクトルの同じ成分 (i＝j) どうしをかけたものの総和を取りました。一方、(1)では異なる成分（i≠j）をかけたものも加えていることに注意してください。

なぜ同じでないかというと、高校数学で習う内積は、正規直交基底（(1,0), (0,1)など）という特別な基底のもとでの内積公式だからです。
一方、(1)は正規直交でない基底にも使える汎用的な内積公式です。

では、(1)から高校数学の内積公式が導出できることを確認して終わりにしましょう。
もしも基底が正規直交であれば、(1)は $g_{ij}=\delta_{ij}, \quad \textbf{e}_i\cdot\textbf{e}_j=\delta_{ij}$ なので
\begin{eqnarray}
d &=& (V^1)^2g_{11}+(V^2)^2g_{22}+\cdots+(V^n)^2g_{nn}\\
&=&\displaystyle \sum_{i}(V^i)^2
\end{eqnarray}めでたく高校数学の内積の公式に一致しましたね。

参考：
・相対論入門 ―時空の対称性の視点から― (フロー式物理演習シリーズ 18)