【相対論】ローレンツ変換の導出

相対性理論の教科書ならだいたい書いてあると思いますが、一応このサイトでもローレンツ変換の導出方法を書いておきます。
（本記事で「ローレンツ変換」と呼んでいるものは厳密には「ローレンツブースト」のことです）

（スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします）

目的は、下記の相対性理論の2大原理を満たすような、
慣性系 K での時空座標 $X(ct,x,y,z)$
と
慣性系 K’ での時空座標 $X'(ct’,x’,y’,z’)$
の関係式を求めることです。

(I) 相対性原理
互いに等速度連動をしているすべての慣性系において、すべての基本的物理法則はまったく同じ形で表わされる。

(II) 光速不変の原理
いかなる慣性系からみても、光の速さは一定値 $c$ である。

結論

ローレンツ変換の式
$$
\left(\begin{array}{c}
ct’ \\ x’ \\ y’ \\ z’
\end{array}\right)
=
\begin{pmatrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}
\left(\begin{array}{c}
ct \\ x \\ y \\ z
\end{array}\right) \ \ \ \left( \beta = \frac{v}{c}, \ \ \gamma = \frac{1}{\sqrt{1-\beta^2}} \right)$$は、2つの慣性系での光の球面波の式
$$K: x^2 + y^2 + z^2 = (ct)^2$$$$K’: x’^2 + y’^2 + z’^2 = (ct’)^2$$について、K系に対するK’系の相対速度を $\vec{v} = (v, 0, 0)$ と設定して $(x,y,z)$ と $(x’,y’,z’)$ の関係式を計算すると出てきます。

問題設定

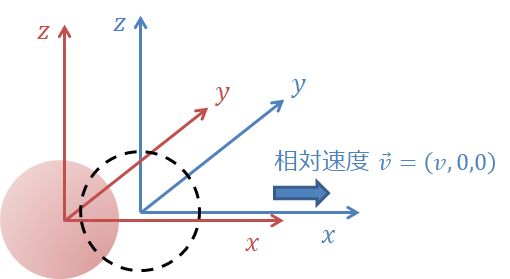
相対速度 $\vec{v}$ で相対運動している 2つの慣性系 K, K’ を考えます。
各時空座標を $X(t, x, y, z), \ X'(t’,x’,y’,z’)$ とします。
慣性系 K と K’ の空間座標の原点が一致したその瞬間を $t=t’=0$ とします。

いまその瞬間に原点から放射された光が真空中を伝わるとします。
このとき、この光の先端の波面を K, K’ それぞれの系上で静止する観測者 A と B が方程式で記述するとどうなるでしょうか。

気をつけることは次の2つです。
(I) 相対性原理により、その光の波面は、両系で同じ形で表現されなければなりません。
(II) 光速不変の原理により、光の速さはいずれの系から見ても同じ値 $c$ です。

結果、こうなります。
$$K: x^2 + y^2 + z^2 = (ct)^2 \tag{1}$$$$K’: x’^2 + y’^2 + z’^2 = (ct’)^2 \tag{2}$$高校数学で習った球面の公式そのままですね。

ここで求めたいのは、
(1)(2)を満たすような $X(t,x,y,z)$ と $X'(t’,x’,y’,z’)$ の関係式
です。

ポイントは 2つ

$X(t,x,y,z)$ と $X'(t’,x’,y’,z’)$ の関係式は、次の2つの事実（仮定ではありません）を元にして求めることが多いです。

① 関係式は　$X’ = A X$ で表される ($A$ は 4×4 の変換行列)　。
　これは変換式とも捉えられる。
② K と K’ の相対速度 $\vec{v}$ は $x$ 成分 $v_x = v$ だけを持つものとしても一般性を失わない。

①の証明・・・例えば下記をご参照ください。この記事では割愛します。
　　　　　　　「あきらめない一般相対論」1.11節
②の証明・・・座標を回転して相対速度が $x$ 方向になるようにとることは常にできるからです。

解法

上記ポイント①②を考慮すると、変換式は次のように書けます。
$$t’ = a_1 t + a_2 x + a_3 y + a_4 z \\
x’ = a_5 t + a_6 x + a_7 y + a_8 z \\
y’ = y \\
z’ = z \tag{3}$$
さらに、$(t,x) = (0,0)$ のときに $(t’, x’) = (0,0)$ であるという条件から
$$a_3 = a_4 = a_7 = a_8 = 0$$が出てきます。

また、K 系から見ると K’ 系の原点は $t$ 秒後に $x=vt$ の位置にあるので、(3)の第2式より $0 = a_5 t + a_6 vt$　が出てきます。
よって
$$t’ = a_1 t + a_2 x \\
x’ = -a_6 vt + a_6 x = a_6 (x-vt) \\
y’ = y \\
z’ = z \tag{4}$$と書けます。

これらを(2)に代入すると、
$$\{a_6 (x-vt)\}^2 + y^2 + z^2 = \{c(a_1 t + a_2 x)\}^2$$これが(1)と一致するには、係数を比較して
$$a_6^2 – c^2 a_2^2 = 1 \\
c^2 {a_1}^2 – v^2 {a_6}^2 = c^2 \\
2 c^2 a_1 a_2 + 2 {a_6}^2 v = 0$$これを解いて $\beta = v/c, \ \ \gamma = \frac{1}{\sqrt{1-\beta^2}}$ とおくと
$$a_2 = -\frac{\beta}{c\sqrt{1-\beta^2}} \\
a_1 = a_6 = \frac{1}{\sqrt{1-\beta^2}}$$これを(4)に代入して第1式の両辺に $c$ をかけると
$$ct’ = \gamma ct – \beta \gamma x \\
x’ = -\beta \gamma ct + \gamma x \\
y’ = y \\
z’ = z$$行列で書くと
$$
\left(\begin{array}{c}
ct’ \\ x’ \\ y’ \\ z’
\end{array}\right)
=
\begin{pmatrix} \gamma & -\gamma \beta & 0 & 0 \\ -\gamma \beta & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}
\left(\begin{array}{c}
ct \\ x \\ y \\ z
\end{array}\right)$$
ローレンツ変換の式が導出できました。（おわり）

参考：
・あきらめない一般相対論