直交行列とユニタリ―行列の性質

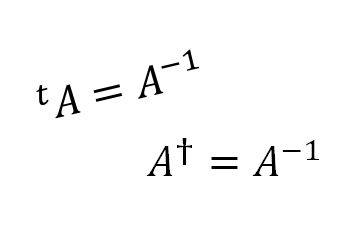
直交行列、ユニタリ―行列、エルミート行列、それぞれどんな行列か、覚えていますか？

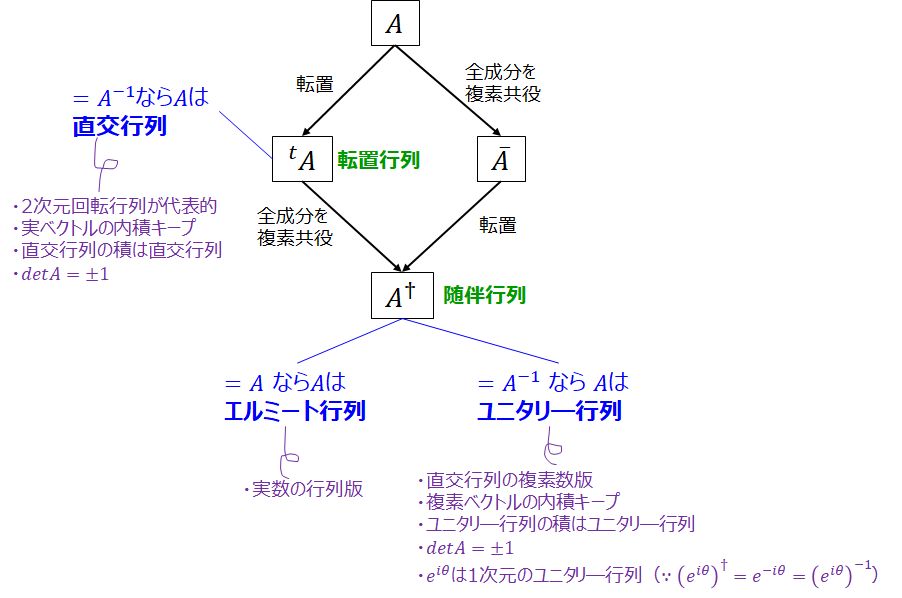
私は下図のように覚えました。

■ 直交行列とその性質

正方行列 $A$ の行の値と列の値を交換した（転置した）行列を $A$ の 転置行列 ${}^t \! A$ と言います。

転置行列が $A$ の逆行列 $A^{-1}$ に等しい場合、$A$ を直交行列といいます。
代表的な例が2次元の座標回転を表す行列です。
$$A=\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}$$
直交行列という名前の由来は、おそらく行ベクトルや列ベクトルが正規直交基底をなすからです（参考：高校数学の美しい物語「直交行列の５つの定義と性質の証明」）。
例えば上の2次元回転行列でしたら、行ベクトルの
$$\vec{e_1} = \begin{pmatrix} \cos{\theta} \\ -\sin{\theta} \end{pmatrix}, \vec{e_2} = \begin{pmatrix} \sin{\theta} \\ \cos{\theta} \end{pmatrix}$$も、列ベクトルの
$$\vec{e_1} = \begin{pmatrix} \cos{\theta} \\ \sin{\theta} \end{pmatrix}, \vec{e_2} = \begin{pmatrix} -\sin{\theta} \\ \cos{\theta} \end{pmatrix}$$も、正規直交基底をなします。

直交行列には、他にも次の性質があります。
・実ベクトルどうしの内積の値を不変に保つ
・直交行列と直交行列の積は直交行列
・行列式の値が $\pm 1$

■ ユニタリ―行列とその性質

${}^t \! A$ の全成分の複素共役をとったものを $A$ の随伴行列 $A^\dagger$ と言います。

随伴行列 $A^\dagger$ は、転置行列 ${}^t \! A$ の複素数バージョンのようなイメージでいいと思います。

転置行列が逆行列に等しいような行列を直交行列と呼んだのと同じように、随伴行列が逆行列に等しいような行列をユニタリ―行列と呼びます。

ユニタリ―行列には他にも次の性質があります。
・複素ベクトルどうしの内積を不変に保つ
・ユニタリ―行列とユニタリ―行列の積はユニタリー行列
・行列式の値が $\pm 1$

ユニタリ―行列のとってもシンプルな例は、$e^{i\theta}$ です。
これは1行1列のユニタリ―行列です。なぜなら、随伴行列が逆行列になっているからです。
$(e^{i\theta})^\dagger = e^{-i\theta} = (e^{i\theta})^{-1}$

■ ついでにエルミート行列

ついでに、随伴行列が自分自身に等しいような行列のことはエルミート行列と呼びます。
詳細は別記事にする予定ですが、実数の行列バージョンのような性質があります。
エルミート行列（演算子）は、例えば量子力学においてはとっても重要な役割を果たします。

まとめると