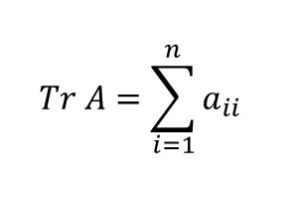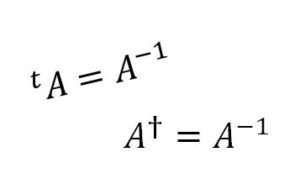ベクトル解析で忘れがちな公式

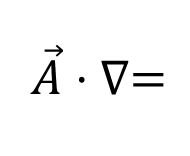
個人的に忘れがちだと思うベクトル解析の公式をメモしておきます。

■ $\vec{A} \cdot \nabla$

$\vec{A} \cdot \nabla$ は $\vec{A} \cdot \nabla = \nabla \cdot \vec{A}$ （$\vec{A}$ の発散）ではなく、次の意味を持つ演算子です。

$$\vec{A} \cdot \nabla = A_1 \frac{\partial}{\partial x} + A_2 \frac{\partial }{\partial y} + A_3 \frac{\partial}{\partial z}$$

■ 勾配、発散、回転に関する公式

(1) $\nabla(\vec{A} \cdot \vec{B}) = (\vec{B} \cdot \nabla)\vec{A} + (\vec{A} \cdot \nabla)\vec{B} + \vec{B}\times(\nabla \times \vec{A}) + \vec{A}\times(\nabla \times \vec{B})$
(2) $\nabla\cdot(\vec{A}\times\vec{B}) = \vec{B}\cdot (\nabla \times \vec{A}) – \vec{A}\cdot(\nabla \times \vec{B})$
(3) $\nabla \times (\nabla f) = \vec{0}, \ \ \nabla \cdot (\nabla\times \vec{A}) = 0$
(4) $\nabla \times (\nabla \times \vec{A}) = \nabla (\nabla\cdot \vec{A}) – \nabla^2 \vec{A}$
(5) $\nabla \times (\vec{A} \times \vec{B}) = (\vec{B}\cdot\nabla)\vec{A} – (\vec{A}\cdot \nabla)\vec{B} + \vec{A}(\nabla \cdot \vec{B}) – \vec{B}(\nabla \cdot \vec{A})$

中でも(3)はよく出てきますね。

・参考：
演習ベクトル解析 (サイエンスライブラリ演習数学 9)