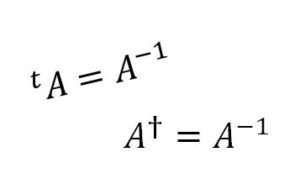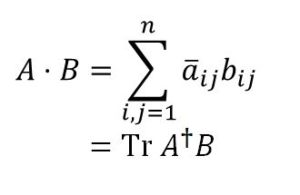群の定義

数学で群 (group) ってのが出てきます。

集合(set) とは違うのでしょうか？

■ 群の定義

「岩波 数学入門辞典」の「群」によると、群の定義（公理）は次のように書かれています。

集合 \(G\) の任意の2元 \(a,b\) に対して　\(a,b\) の積と呼ばれる \(G\) の元がただ1つ定まり（この元を \(ab\) と表す）次の性質を持つとき群という。
(1）
積に対して結合法則が成り立つ。
すなわち \(G\) の任意の元 \(a,b,c\) に対して \((ab)c = a(bc)\) が成り立つ。
(2）
単位元が存在する。
すなわち \(G\) のすべての元 \(a\) に対して \(ae=ea=a\) となる元 \(e\) が存在する。\(e\) を単位元という。
(3)
任意の元 \(a\) に対して \(ab=ba=e\) となる \(G\) の元 \(b\) が必ず存在する。\(b\)を\(a\)の逆元といい、\(a^{-1}\) と表す。

つまり群は集合の特別な場合ってことですね。

■ 群の例

例えば2次元の座標回転を表す行列
$$A=\begin{pmatrix} \cos{\theta} & \sin{\theta} \\ -\sin{\theta} & \cos{\theta} \end{pmatrix}$$で\(\theta\) の値が異なるものの集合を考えます。
積を行列の積の演算方法で定義すると、この集合は下記より群の条件を満たします。

(1) 結合法則： \(A(BC)=(AB)C\)
(2) 単位元\(E\)が存在する： \(AE = EA = A\)
(3) 逆元\(A^{-1}\)が存在する： \(AA^{-1}=A^{-1}A=E\)

■ 群でないものの例

例えば、3次元実ベクトルの集合に対して、積として外積を採用すると、一般に外積は結合法則が成り立たないので、群ではありません。


参考：
キーポイント行列と変換群 (理工系数学のキーポイント (8))