【線形代数】添え字での行列計算に慣れる方法

行列の計算は、まずは成分を１つ１つ書くことから学ぶと思います。

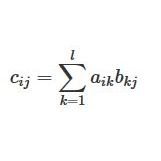
例えばこんな感じ↓
$$
A = \left(
\begin{array}{cc}
a_{11} & a_{12} \\
a_{21} & a_{22} \\
\end{array}
\right),
B = \left(
\begin{array}{cc}
b_{11} & b_{12} \\
b_{21} & b_{22} \\
\end{array}
\right),C = AB$$とすると
$$C = \left(
\begin{array}{cc}
a_{11}b_{11}+a_{12}b_{21} & a_{11}b_{12}+a_{12}b_{22} \\
a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \\
\end{array}
\right)$$
2×2行列の掛け算なら成分数が少ないのでまだいいですが、4×4、5×5・・・となると気が遠くなるほど面倒くさくなりますよね。

ルールに従って機械的に埋めていくだけなのに。

途中で書き間違える可能性もありますし。

そういうときに便利なのが添字表記です。

上の例なら、
$$
c_{ij} = \sum_{k=1}^2 a_{ik}b_{kj}
$$さらに一般的に A を n×l, Bを l×m の大きさとしても
$$
c_{ij} = \sum_{k=1}^\color{red}{l} a_{ik}b_{kj}
$$と1行で書けてしまいます。
行列の積 AB は A の列数とBの行数が一致していないと計算できません。
このことに対応して、a の2つめの添字とbの1つ目の添字 k が一致しています。

しかしながら、1行で書けてすっきりはしたものの、添字が i, j, k, l の4つも出てくるうえに２次元のグラフィカルな見た目もなくなってしまったので、直感的にわかりにくくなってしまうことも否めません。

なのでケースバイケースで使い分けるのがいいと思います。

「使い分ける以前に添字形式の計算に慣れていないので添字形式でなんて書けない」という方もいるかもしれません。

以前の私がそうでした。

これはもう、練習して慣れるしかありません。

添字形式の計算が効果的に身につく演習書で私がおススメなのはこちらです↓