正方行列の対角和（トレース）の性質

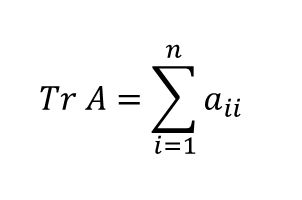
正方行列の対角和（トレース）の定義と性質をメモしておきます。

■ トレースの定義

トレースとは、n次元正方行列 $A=[a_{ij}]$ の対角成分の和 $a_{11} + a_{22} + \cdots + a_{nn}$ のことです。
（出典：岩波数学入門辞典）

$\mathrm{ tr }\ A$ や $\mathrm{ Tr }\ A$ と書きます。

■ トレースの性質

トレースには下記の性質があります。

(1) $\mathrm{ Tr }\ (A+B) = \mathrm{ Tr } \ A + \mathrm{ Tr } \ B$
(2) $\mathrm{ Tr } \ (\alpha A) = \alpha \ \mathrm{ Tr } \ A$ ($\alpha$ は複素数)
(3) $\mathrm{ Tr } \ AB = \mathrm{ Tr } \ BA$
(4) $\mathrm{ Tr } \ MAM^{-1} = \mathrm{ Tr } \ A$

・(1) の証明
$$\mathrm{ Tr }\ (A+B) = \sum_{i=1}^{n}(a_{ii} + b_{ii}) = \sum_{i=1}^{n}a_{ii} + \sum_{i=1}^{n}b_{ii} = \mathrm{ Tr } \ A + \mathrm{ Tr } \ B$$
・(2)の証明
$$\mathrm{ Tr } \ (\alpha A) = \sum_{i=1}^{n} \alpha a_{ii} = \alpha \sum_{i=1}^{n}a_{ii} = \alpha \ \mathrm{ Tr } \ A$$
・(3)の証明
$$\mathrm{ Tr } \ AB = \sum_{i=1}^{n} \ (AB)_{ii} = \sum_{i=1}^{n} \sum_{j=1}^{n} a_{ij} b_{ji} = \sum_{j=1}^{n} \sum_{i=1}^{n} b_{ji} a_{ij} = \mathrm{ Tr } \ BA$$
・(4)の証明
(3)を使って
$$\mathrm{ Tr } \ MAM^{-1} = \mathrm{ Tr }\ (MA)M^{-1} = \mathrm{ Tr } \ M^{-1}{MA} = \mathrm{ Tr } \ A$$

参考：
キーポイント行列と変換群 (理工系数学のキーポイント (8))