内積の性質はそれほど当たり前でもない

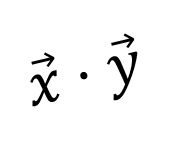
2次元ベクトルの内積（スカラー積）は次のように定義されます。

\(\vec{x}=\left( \begin{array}{c} x_1 \\ x_2 \end{array} \right), \vec{y}=\left( \begin{array}{c} y_1 \\ y_2 \end{array} \right)\) として \(\vec{x}\cdot \vec{y} = x_1 y_1 + x_2 y_2\)

そして内積には次の性質があるということがだいたいの教科書には書いてあります。

(1) \(\vec{x}\cdot \vec{y} = \vec{y} \cdot \vec{x}\)　（交換法則）
(2) \((\vec{x}+\vec{y})\cdot \vec{z} = \vec{x} \cdot \vec{z} + \vec{y} \cdot \vec{z}\)　（分配法則）
(3) \((a \vec{x}) \cdot \vec{y} = a (\vec{x} \cdot \vec{y})\), \(a\) は実数
(4) \(\vec{x} \cdot \vec{x} \ge 0\)
(5) \(\vec{x} \cdot \vec{x} = 0\) ならば \(x=0\)

(1)～(5)それぞれに内積の定義式を代入すれば、たしかに成り立つことが確認できます。


ただ、(1)～(5)の式を見ても「ふーん。当たり前じゃないの？」と思われる方も多いのではないでしょうか。

ここで、私なりの鉄則があります。それは

「当たり前だと思うときは、成り立たない場合を考えよう」

ということです。成り立たない場合を経験して、はじめて成り立つことのありがたさがわかるというわけです。

例えば内積の定義が \(\vec{x}\cdot \vec{y} = x_1 y_1 + x_2 y_2\) ではなく \(\vec{x}\cdot \vec{y} = x_1 + y_2\) だったとするとどうでしょうか？

\(\vec{x}\cdot \vec{y} = x_1 + y_2\) の場合、下記に示すように(1)～(5)は成り立たなくなります。

(1)
\(\vec{y} \cdot \vec{x} = y_1 + x_2 \ne \vec{x} \cdot \vec{y}\)

(2)
左辺は \((\vec{x} + \vec{y})\cdot \vec{z} = x_1 + y_1 + z_2\)
右辺は \(\vec{x}\cdot \vec{z} + \vec{y} \cdot \vec{z} = x_1 + z_2 + y_1 + z_2 = x_1 + y_1 + 2z_2\)

(3)
左辺は \((a\vec{x}) \cdot \vec{y} = ax_1 + y_2\)
右辺は \(a(\vec{x}\cdot\vec{y}) = a(x_1 + y_2)\)

(4)
左辺は \(x_1 + x_2\) なので \(\ge 0\) とは限りません。

(5)
\(\vec{x} \cdot \vec{x} = x_1 + x_2 =0\) これは例えば \(\vec{x}=\left( \begin{array}{c} 2 \\ -2 \end{array} \right)\) でも成り立ちます。


このように、成り立たない場合を考えることによって、(1)～(5)はそれほど当たり前の性質ではなく、内積の定義が \(\vec{x}\cdot \vec{y} = x_1 y_1 + x_2 y_2\) だからこそ成り立つ性質だということが実感できると思います。




参考：
キーポイント行列と変換群 (理工系数学のキーポイント (8))