極座標で円の面積を求める方法の補足

■ dr^2 の積分が必要？

円の面積を求める方法の1つに、2次元極座標で \(r\) 方向と \(\theta\) 方向の格子に分割して、
$$S=\int_0^R \int_0^{2\pi} r dr d\theta \tag{1}$$を計算する方法がありますよね。

この場合、積分する微小領域の形を縦と横が \(dr\) と \(rd\theta\) の長方形とみなして、その積 \(r dr d\theta\) をその面積としていると見なせます。

しかし微小領域は厳密には長方形ではなく、大きな扇形から小さな扇形を引いたような形です。

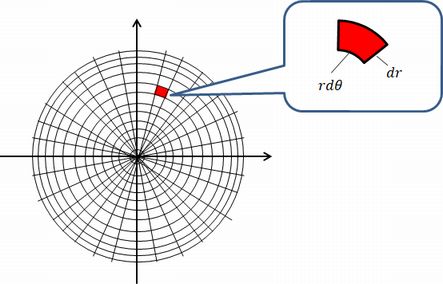
これをきちんと計算すると、赤い微小領域の面積は

(大きな扇形の面積) － (小さな扇形の面積)
$$=\left\{\pi(r＋dr)^2 – \pi r^2\right\} \frac{d\theta}{2\pi} = r dr d\theta + \frac{1}{2}dr^2 d\theta \tag{2}$$となります。

この段階で「2次の微小量は無視して」として第2項をゼロとしているのを見ることがあります。が、第2項は微小量とはいえこれから積分するので、本当にゼロとしていいのか不安になりませんでしょうか？

さらに「数学なのに近似するのか？」という誤解を与えかねないような気もします。

というわけで、第2項を残したまま円全体の面積を求めます。
(2) を r と θ で積分して
$$S=\int_0^R \int_0^{2\pi} {r dr d\theta}+\int_0^R \int_0^{2\pi} {\frac{1}{2}dr^2 d\theta}$$となります。
第 1 項は (1) の右辺と同じですね。
(1)を計算すると正しい結果が得られることは知られているので、第 2 項 がゼロになるはずなのですが、\(dr^2\) の積分ってどうやればいいのでしょうか？

（この疑問もQ&Aサイトで質問して下記のように納得できました。）


■ ウマい回避法があります

この事態をウマく回避する方法があります。

それは、赤い微小領域の面積を下図のように \(dr\) を \((1/2)dr\) ずつに切って考えることです。


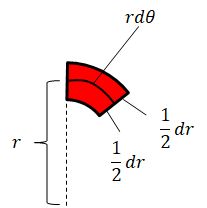
すると赤い微小領域の面積は

(大きな扇形の面積) － (小さな扇形の面積)
$$=\left\{\pi\left(r＋\frac{1}{2}dr \right)^2 – \pi \left( r-\frac{1}{2}dr \right)^2\right\} \frac{d\theta}{2\pi} = r dr d\theta$$となり \(dr^2\) は出てこずに(1)と一致する結果が得られます。