特殊相対性理論では時間と空間が…
【相対論】 不変距離や固有時とは、観測される物体自身にとっての距離や時間のこと

特殊相対論では、時空における2つの事象 A, B 間の距離 \(ds\) は
$$(ds)^2 = (cdt)^2 – \left\{ (dx)^2 + (dy)^2 + (dz)^2\right\} \tag{1}$$と表されます。「世界距離」「世界間隔」「不変距離」などと呼ばれています。
本によっていろいろ方言(定義方法の違い)はあるものの(詳しくはこちらにまとめてあります)、時間の2乗に関する項と空間の距離の2乗項が異符号であることは共通しています。
どうして「時間の2乗」と「空間の距離の2乗」を異符号にして足し合わせたものを「時空の距離」と定義するんでしょうか?
私の手元にある多くの教科書では、(1)がどこから出てきたかの説明はなく、突然
「(1)という量を定義すれば、これはどの慣性系でも同じ値になる。これを世界距離と呼ぶ。」
と書かれています。
でもそれだと
「たまたま、ローレンツ変換しても不変な量 (1) を思いついた」
という具合に読めてしまいませんでしょうか?
「背景の説明は不要。そうなんだから仕方がない」と言われればそれまでですが、何らかの背景があって (1) の量が導出されたと考えるのが自然じゃないでしょか。では (1) の式はいったいどこから出てきたんでしょうか?
私なりの理解を書いてみます。
(スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします)
結論
結論としては、不変距離とは、 事象 A, B を結ぶ慣性系、つまり観測される物体自身にとっての距離や時間のことで、不変距離を考える背景は、それを採用すれば便利だからだと思います。特殊相対論によると、同じ時空上の距離 \(ds\) であっても、その時間や距離の値は観測する慣性系によって異なります。
そこで、 「\(ds\) を辿る慣性系自身から見た距離や時間」であれば、どの慣性系から見ても同じ値のはずなので、それを全慣性系(観測者)の共通言語にすれば便利そうですよね。
これが不変距離を考えた背景だと思います。
では、不変距離の定義式 (1) が、 観測される物体自身にとっての距離や時間を表していることを導出してみましょう。
導出
例えば次のような状況を考えます。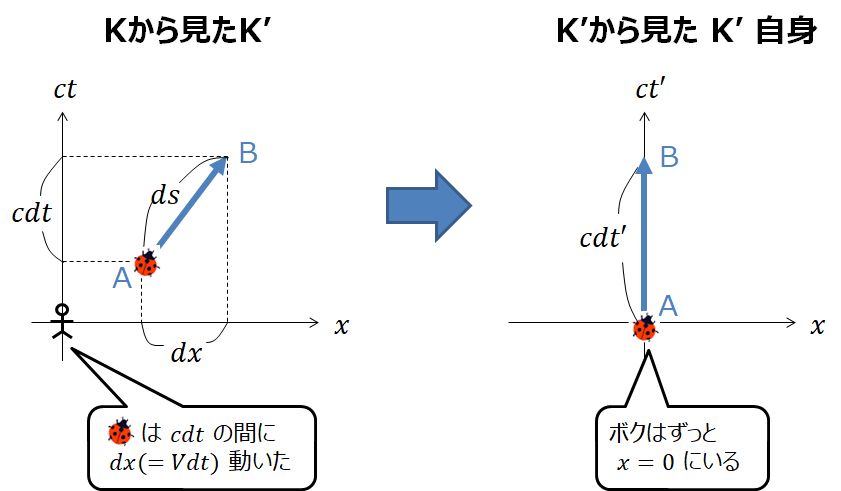
左側のグラフは、人間から見たテントウ虫の軌跡を描いた時空図です。テントウ虫は \(ds\) 上をたどります。この人間から見た慣性系を K とします。
一方右側のグラフは、人間に観察されているテントウ虫から見た自分自身の軌跡を描いた時空図です。このテントウ虫から見た慣性系を K’ とします。
ここで、一般に微小距離に関するローレンツ変換は次のように書けます。
$$
\left(\begin{array}{c}
cdt’ \\ dx’
\end{array}\right)
=
\begin{pmatrix} \gamma & -\gamma \beta \\ -\gamma \beta & \gamma\end{pmatrix}
\left(\begin{array}{c}
cdt \\ dx
\end{array}\right) \tag{3}$$このローレンツ変換を、上記の慣性系 K から慣性系 K’ への変換に適用します。
K から見た事象AとBを結ぶベクトル \(\left(\begin{array}{c}cdt \\ dx\end{array}\right) \) は、 K’ にとっては \(\left(\begin{array}{c}cdt’ \\ 0\end{array}\right) \) になるはずです。
K’ にとってのベクトルの x成分がゼロである理由は、Kが観測しているのは K’ で、K’にとって自分は常に空間座標の原点にい続けるからです。
このことを(3)を使って式で書くとこうなります。
$$cdt’ = \gamma (cdt – \beta dx) \tag{4}$$$$0 = \gamma (dx – \beta cdt) \tag{5}$$
まず(5)から見てみましょう。
\(dx = vdt\) を用いて右辺を計算すると、
$$\gamma (dx – \beta cdt) = \gamma (dx – \frac{v}{c} cdt) =\gamma (dx – vdt) = 0$$となり、たしかに等号が成り立っています。
次、(4)も計算してみましょう。
$$cdt’ = \gamma (cdt – \beta dx) = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} (cdt – \frac{v}{c}dx) \\
= \sqrt{\frac{(c^2dt – vdx)^2}{c^2 – v^2}}$$ここで \(v = \frac{dx}{dt}\) を代入すると
$$=\sqrt{\frac{(c^2dt – \frac{dx^2}{dt})^2}{c^2 – (\frac{dx}{dt})^2}} \\
= \sqrt{\frac{(c^2dt^2 – dx^2)^2}{c^2dt^2 – dx^2}} = \sqrt{c^2 dt^2 – dx^2}$$両辺を2乗すると
$$(cdt’)^2 = c^2 dt^2 – dx^2$$右辺に \(c^2 dt^2 – dx^2\) という、今まさに問題にしている世界距離の定義式が出てきました!(^^)
参考:
・高校数学でわかる相対性理論 (ブルーバックス)

・相対性理論 (物理入門コース (9))

1