【相対論】時空図（ミンコフスキー図）を描く練習

まず「時空図とは？」について説明して、そのあと時空図の中に世界線を書き込む練習をします。

時空図とは？

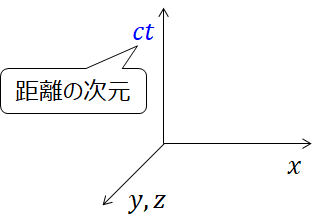
相対性理論で、時空図（またの名をミンコフスキー図）というのが出てきます。
上の図のようなやつですね。

「時空図」なんて聞くと「なんだか難しそう」と思われるかもしれませんが、なんてことはありません。
高校物理の力学で、横軸に時間 (t)、縦軸に距離 (x) をとったグラフを描いたことがあるかと思います。あれとほとんど同じです。

違いは下記くらいですね。

・時間 t には光速 c をかけて ct とすることで、次元（単位）を距離と同じにする
・ct 軸は縦に書く

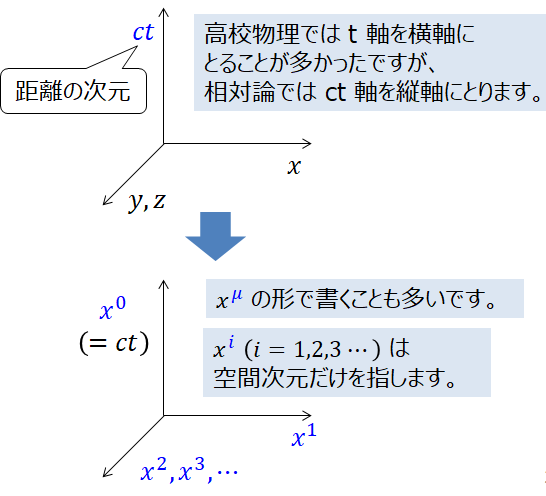
ちなみに・・・
・ct 方向成分は「第 1 成分」ではなく「第 0 成分」と書かれることが多く、成分は \((x^0, x^1, x^2, x^3,…)\) のように表されます。
・時空図の座標系の取り方を「ローレンツ座標系」と呼ぶことがあります。

練習問題

では基本を押さえたところで、次の練習問題を解いてみましょう。

(Q1) t = 0 に x = 0 を出発した点粒子の1次元運動について、次の (1) から (3) の軌跡 (「世界線」) を下図に書き込んでください。（縦軸と横軸のスケールは同じとして）
　　　(1) 速度が c の場合
　　　(2) 速度が c/2 の場合
　　　(3) 速度が c 以下で変動する場合

(Q2) (2) 光速以下の粒子が通りうる領域を斜線で示してください。

まず (Q1) について。どう考えたらいいでしょうか。
ヒントとしては、例えば 1　秒後を考えてみたらどうでしょう？
さらに高校物理の x-t グラフ（横軸 t, 距離 x）で考えるとわかりやすいかも。

答えはこんな感じになります↓