開催日時毎週 火・金 朝 06…
【相対論】双子のパラドックスのモヤモヤをスッキリさせましょ

相対論の入門書に必ずと言っていいほど出てくる「双子のパラドックス」。
私なりにすっきり腑に落ちた説明をメモしておきます。
双子のパラドックスとは?
まず、一応双子のパラドックスとはどういうものか説明しておきます。こんなパラドックスです。双子のうちの A さんが地球に残り、もう一方の B さんが宇宙船で光速に近い速度で宇宙旅行をして帰ってくると、B さんの時計は A さんよりも遅れる。これは事実。
しかし相対論が「すべての速度は相対的」というのなら、B さんから見た A さんも同じ動きをするはずなので、どちらか一方だけ年をとるのはおかしくないか?どういうことよ??
もっともな疑問ですよね。
このパラドックスの解説として、よく加速度が云々という説明を見かけます。
「B さんは宇宙のどこかで折り返す必要がある。そこで加速度が働くので、パラドックスは解決する。」というものです。
私はこの加速度を使った説明ではまったく腑に落ちませんでした。
具体的には以下の疑問が残りました。
・A さんから見るとたしかに B さんは折り返し地点で加速するけど、B さんから見れば A さんが加速するのでは?
・加速度が働く物体を外から見ると時間がゆっくり流れるらしいが、それでどう解決するのか?
・不連続に突然折り返せると仮定したらどうなるのか?
結論:
「宇宙船の往路と復路では慣性系が異なる」ことがポイント
結論からいうと、B さんの時計が遅れる理由を考えるうえでポイントとなるのは、「宇宙船の往路と復路では慣性系が異なる」ことです。(それを加速度といえばそうなのですが、ちょっとニュアンスが異なりますよね(^^;)
そのことを踏まえて、時空図(ミンコフスキー図)を書いて、実際に固有時を計算すると納得できます。
<用語説明>
・時空図・・・横軸に空間、縦軸に ct (光速 × 時間) を取って、ある慣性系から見た、観測対象の物体が時空上のどこに位置するかをグラフ化したもの。
・固有時・・・観測対象の物体にとっての時間。(詳細はこちらの記事を参照。)
A さんの慣性系で考えた場合と B さんの往路の慣性系から見た場合に分けて、どちらで考えても B さんの時計が遅れることを証明します。
A さん(地球に残る方)から見た場合の固有時間
A さんの慣性系からみた時空図は下記のようになります。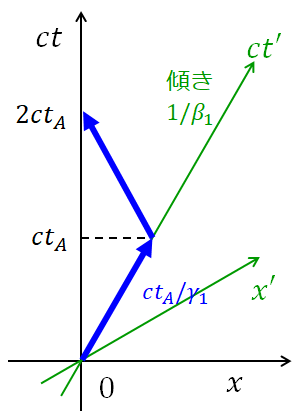
青い2本の矢印が B さんの軌跡です。地球から B さんが出発した地点を原点にとってます。
A さんにとって、B さんが帰ってくるまでに経過した時間を A さんの時計で測ったもの (A さんの固有時間) は、A さん自身は ct 軸に沿って進みますので、\(2ct_A\) です。
一方B さんの固有時間は、上図より \(2ct_A/\gamma_1\) です。(詳細は最後の参考資料などをご覧ください。)
(\(\gamma_1=1/\sqrt{1-(\beta_1)^2}, \beta_1=V/c,\) \(V\)は宇宙船の速度)
A さんの固有時間 \(2ct_A\) と B さんの固有時間 \(2ct_A/\gamma_1\) を比べると、
\(2ct_A-2ct_A/\gamma_1>0\)
より、A さんの固有時間の方が大きいので、B さんの時計は A さんの時計よりも遅れることがわかります。・・・(1)
B さん(宇宙旅行して帰ってくる方)から見た場合の固有時間
一方、B さんの往路の慣性系からみた B さんの軌跡は下記の青矢印のようになります。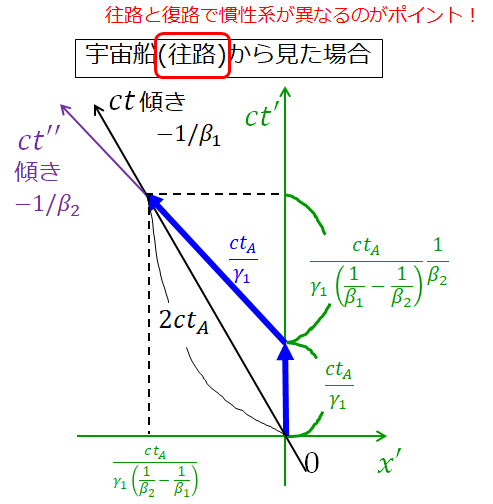
B さん自身は折り返し地点までは ct’ 軸に沿って進みますので、出発から折り返し地点までの B さんの固有時間は、\(ct_A/\gamma_1\) です。
次に B さんの復路は、B さんは異なる慣性系に移ってしまいますので、B さんの往路の慣性系に備え付けたカメラで、B さんを追うことにします。 すると、復路にかかる B さんの固有時間は、これまた \(ct_A/\gamma_1\) であることがわかります。
一方 A さんの固有時間は、図に書いたとおり、\(2ct_A\) です。
A さんと B さんの固有時間を両者を比べると、
\(2ct_A-2ct_A/\gamma_1>0\)
より、A さんの固有時間の方が大きいので、B さんの時計は A さんの時計よりも遅れることがわかります。・・・(2)
(1)(2) より、A さんの慣性系・Bさんの往路の慣性系のどちらで考えても、2人が別れてから再開するまでに経過する A さんの固有時間は \(2ct_A\) 、B さんの固有時間は \(2ct_A/\gamma_1\) となりました。
そしてどちらの慣性系で考えても、B さんの帰還時、B さんの時計は A さんのものより遅れることが証明できました。
下記の本をかなり参考にさせてもらいました。
6