地上を慣性系とみなせるのは地球の質量がデカいから

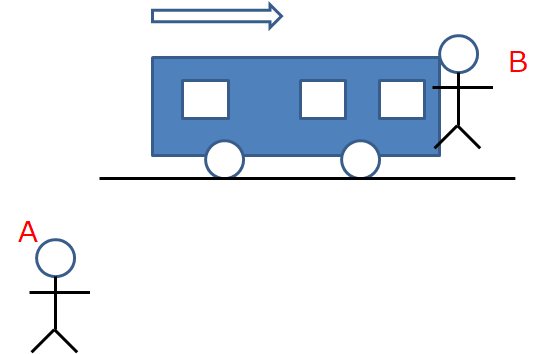
A 君は地上にいるとします。B 君は加速中の電車に乗っているとします。
A 君から見て動いているのは電車だけで、その他の景色は動いてないように見えるとします。
さらに B 君がその電車に乗っていて、外の景色を見ながら、電車の中でボールを落とすとします。
このとき、A君は慣性系、B君は非慣性系にいるのだといろんな本などに書いてます。

しかしみなさん不可解に感じないでしょうか。
私は長い間、次の疑問が頭から離れませんでした。
「静止・加速はあくまで相対的なもので、B 君から見れば A 君が加速していて対等なはずなのに、なぜ B 君だけが慣性系ではなくなるんだろう？」

それについての今の私の考えはこうです。

厳密には A 君も B 君も慣性系ではない。
（なので上で「答えは・・・」と書いた内容は厳密には間違い。）
だけど「A 君のいる地球の質量」 >> 「B 君のいる電車の質量」だから近似的に A 君だけ慣性系とみなせる。

どういうことか、順を追ってお話します。

■ 電車が等速直線運動しているときは？

そもそも、慣性系って何でしょう？
例えば岩波理化学辞典では、「ニュートンの運動法則が成り立つ座標系」とあります。
ニュートンの運動法則とは、 \(ma = F\) ですね。
\(F = 0\) なら、\(a = 0\)、つまり静止または等速直線運動を続けます。

では、まずは電車が直線運動しているとしましょう。
電車は厳密には車輪とレールの静止摩擦力で動きますが、ここでは摩擦 0 で滑っているとします。
A 君、B君はそれぞれ慣性系でしょうか？

答えは、2人とも慣性系です。
理由を考えます。
まず A 君から見ると、電車は外から力が加わってなくて、かつ等速直線運動をしています。つまり \(ma = F\) を満たしています。
さらに電車以外の景色も、外力の合力が 0 で静止しているので、 \(ma = F\) を満たしています（\(a=F=0\)）。
よって、A 君は慣性系です。
次に B 君はというと、B 君から見た外の景色は、外力の合力が 0 で等速運動しているので、 \(ma = F\) を満たしています。
また、落としたボールは重力で自由落下するので \(ma = F\) を満たしています。
よって、B 君も慣性系です。

■ 電車が加速度運動しているときは？

では次に、電車が加速中の場合はどうでしょうか。
ここで電車は、動力を得て回転する車輪とレールの間の静止摩擦力で加速しているとします。
A 君、B君はそれぞれ慣性系でしょうか？

答えは、A 君は慣性系ですが、B 君は慣性系ではありません。
まず A 君から見ると、電車も風景も、 \(ma = F\) で説明できるのはいいでしょうか。
次に B 君から見ると、外の景色は、力を受けてないにも関わらず加速しているように見えます。
また、落としたボールも真下に落ちずに斜めの方向に落ちます。水平成分が \(ma = F\) では（「慣性力」なるものを持ち出さないかぎり）説明できませんね。
なので B 君は慣性系ではありません。

■ 地上を慣性系とみなせるのは、考えている系に対して地球の質量がデカいから

ここで、最初の疑問に戻ります。
「静止・加速はあくまで相対的なもので、B 君から見れば A 君が加速していて対等なはずなのに、なぜ B 君だけが慣性系ではなくなるんだろう？」

車輪とレールの摩擦力で電車が加速するということは、同時に地球はレールを介してその反作用となる力を受けているはずです。
しかし地球の質量は電車の質量と比べてあまりにも大きいので、地球が反作用によって得る加速度は、電車の加速度と比べればほぼゼロ。
そのため、A 君から見た電車の加速度は、\(a = F/m\) (\(m\) は電車の質量) とみなせて A君は慣性系、ということで納得しました。

長年の疑問が解けてすっきり。