虚数をイメージする方法

2乗すると ―1 になる数、虚数。
英語では「imaginary number (想像上の数)」、日本語でも「虚数」となんだか実在しない数のようで、とらえどころがないように感じている方もいらっしゃるのではないでしょうか。

この記事では、虚数（複素数）を直観的（物理的）にイメージする方法をご紹介します。
（既にあるかもしれませんが一応オリジナルのつもりです(^^;)

それは、次のように想像することです。

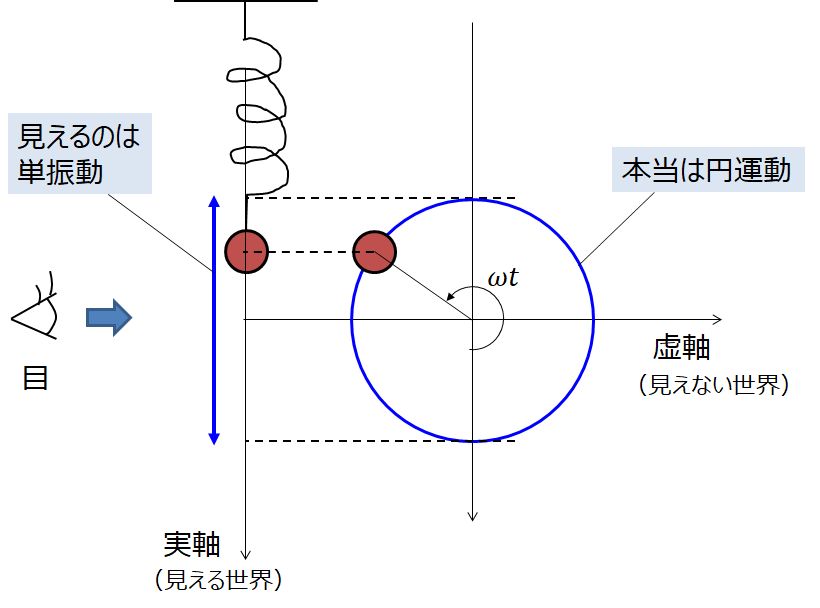
バネの振動は、バネの背後に見えない奥行きがあって、実は円運動している。
それを真横から見ているので単振動に見えるだけ。
「見えない奥行き」が虚数軸。

図に書くとこんな感じです↓


こちらに同じような系のアニメーションを作ってくださってる方もいます。


もう少し言葉で説明しますね。

上の図のように、目の前でおもりのついたバネが振動（単振動）しているところを想像してください。

それは式で書くと
$$y = A \cos{\omega t}$$と書けると高校物理で習ったと思います。

でもこれって不思議に感じたことはないでしょうか？
なんでバネの動きが三角関数に従うんだ？と。

ま、「微分方程式を解けばそうなる」と言われればそれまでなんですが、結果だけを見るとなんだか不思議です。

そこで、見えない軸がその奥に広がっていると考えます。
それを虚数軸とします。見えないのでまさに虚数っぽいですよね。

すると、\(y = A \cos{\omega t}\) という式は、
$$z = A \left(\cos{\omega t} + i \sin{\omega t}\right)$$ という複素平面上の円運動の実部、つまり実軸への正射影を表していることになります。

で、私たちに見えるのはこの実軸に射影された世界なのだととらえるんです。
（この見方の妥当性は、力学の問題を解く際に複素数まで範囲を広げて考えて、最後に実部を取れば正解が得られることに裏付けられていると考えています。）

このように「単振動の正体は円運動で、見えない奥行き方向を虚数軸と考える」というのが虚数のイメージのひとつの提案です(^^)。


ここから先はやや妄想です。

このとき、虚数軸は便宜上考えているだけではなく、実在しているけど私たちが感知できていないだけということはありませんかね？
確認する手段はないと思いますが、否定もしきれないのではないでしょうか？

個人的な感覚としては、単振動（三角関数）よりも円運動の方が自然界の動きとしてありそうな気がします。
ヒモにおもりをつけて振り回せば円運動になるのは不思議ではないので。

大学の力学や電気回路の教科書で、「解を複素数と置いて解いて、最後に実部だけとる」という方法がとられることがあります。それは計算を簡単にするための「テクニック」とされることが多いですが、実は虚部を切り捨てる前の複素数の解こそが自然の正体なのかも？なんて考えてしまいます。
（変なこと言ってたらご指摘ください m(_ _)m）