■ 古典的な物理量の量子化に挑…
【交換子】 [A, B] と [A, 1/B] の関係は?
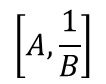
量子力学で演算子 \(A\) と演算子 \(B\) の交換関係を \([A,B]\) と書きます。
では \(B\) の逆演算子を \(\frac{1}{B}\) と書くとすると、\([A, \frac{1}{B}]\) の値はどうなるでしょうか?
こんな風に変形します。
\begin{eqnarray}
\left[A, \frac{1}{B}\right] &=& A\frac{1}{B} – \frac{1}{B}A \\
&=& \frac{1}{B}B A\frac{1}{B} – \frac{1}{B}A B\frac{1}{B}\\
&=& \frac{1}{B} \left(BA\frac{1}{B} – AB\frac{1}{B}\right)\\
&=& \frac{1}{B} \left(BA – AB\right)\frac{1}{B}\\
&=& \frac{1}{B}[B, A]\frac{1}{B}
\end{eqnarray}
つまり
$$\left[A, \frac{1}{B}\right]=\frac{1}{B}[B,A]\frac{1}{B}$$の関係があります。
ですので、例えば \([A, B]=0\) なら \(\left[A, \frac{1}{B}\right]=0\) です。
1

