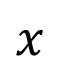「ベクトルを矢印で書くのは高校…
【ベクトル解析】 これだけは押さえておこう!
ベクトル解析では、はじめに場についての下記3つの演算を習うことが多いと思います。
・grad (グラディエント / 勾配)
・div (ダイバージェンス / 発散 / 湧き出し)
・rot (ローテーション / 回転)
その際、特に重要と思われる事柄を挙げておきます。
■ スカラー場とベクトル場、どちらに対する演算か?
まずは各演算の入力についてです。
grad はスカラー場、div と rot はベクトル場に対する演算であることをおさえてください!
■ 要するにそれぞれ何を計算するのか?
次は各演算の出力についてです。
- grad・・・スカラー場において、各座標でのそのスカラー値の最大傾斜の向きと大きさを計算する演算子です。計算結果はベクトルとして出力されます。
- div・・・ベクトル場において、各座標でのそのベクトルの湧き出し量を計算する演算子です。計算結果はスカラーとして出力されます。
- rot・・・ベクトル場において、各座標での渦の強さと向きを計算する演算子です。計算結果はベクトルとして出力されます。
2次元のベクトル場の場合は、rot が出力するベクトルは上記の理由から一般にはその2次元面内には収まらない向きになります。
「これだけは押さえておこう」という内容は以上です。
■ 混乱を招きかねない表現もある
① \((\boldsymbol{u}\cdot\nabla)\boldsymbol{v}\)
ベクトル解析の公式などに\((\boldsymbol{u}\cdot\nabla)\boldsymbol{v}\)というのが出てきます。一見 \(\boldsymbol{v}\) というベクトル場に grad がかかっていて上の記述に矛盾するように見えるかもしれませんが、実際は下記の意味です。
$$(\boldsymbol{u}\cdot\nabla)\boldsymbol{v}
=\left(u_x \frac{\partial}{\partial x}
+ u_y \frac{\partial}{\partial y}
+ u_z \frac{\partial}{\partial z}
\right)\boldsymbol{v}$$つまり次の3つの式を表しています。
$$\left[(\boldsymbol{u}\cdot\nabla)\boldsymbol{v}\right]_x
=\left(u_x \frac{\partial}{\partial x}
+ u_y \frac{\partial}{\partial y}
+ u_z \frac{\partial}{\partial z}
\right)v_x\\
\left[(\boldsymbol{u}\cdot\nabla)\boldsymbol{v}\right]_y
=\left(u_x \frac{\partial}{\partial x}
+ u_y \frac{\partial}{\partial y}
+ u_z \frac{\partial}{\partial z}
\right)v_y\\
\left[(\boldsymbol{u}\cdot\nabla)\boldsymbol{v}\right]_z
=\left(u_x \frac{\partial}{\partial x}
+ u_y \frac{\partial}{\partial y}
+ u_z \frac{\partial}{\partial z}
\right)v_z\\
$$② \(\Delta \boldsymbol{v}\)
\(\Delta \boldsymbol{v}\) についても同様に下記の意味です。
$$\left[\Delta \boldsymbol{v}\right]_x
=\left[\nabla\cdot\nabla \boldsymbol{v}\right]_x
=\left( \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} \right)v_x\\
\vdots$$誤解を生まない書き方をすると、\(\Delta \boldsymbol{v}=\nabla(\nabla \cdot \boldsymbol{v}) – \nabla \times \nabla \times\boldsymbol{v}\) となります。
参考:
・【動画】慶應大学 理工学部 講義 数理物理 第一回
0