======(2018.04.…
区分求積法を証明してみる
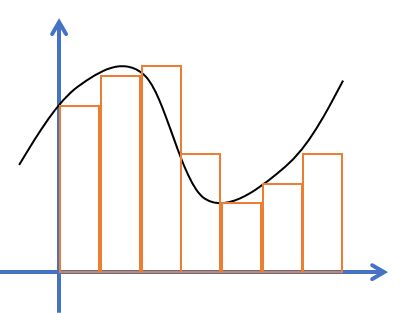
高校数学の教科書には証明が載っていない(らしい)区分求積法。
単調増加関数や単調減少関数なら「はさみうち法」が使えるのですが、そうでないと「はさみうち法」も単純には使えません。
本によっては「左辺と右辺をイコールでつなぐ理由がない」とまで書かれています。
「区分求積法 証明」というキーワードで、以前書いたこの記事にアクセスされる方がパラパラいらっしゃるようですが、他サイトのちょっと本格的な証明へのリンクを紹介しているだけでしたので、高校生にも理解できそうな証明をオリジナルで考えてみました。
こんなカンジでどうでしょうか?↓
(スマホでご覧の方で式の右側がはみだして表示される場合は、式を左右にドラッグすればスクロールします)
■ 問題
区分求積法の公式
$$\lim_{n\to \infty} {\frac{b-a}{n} \sum_{k=0}^{n-1} f\left( a + k \frac{b-a}{n} \right)} = \int_a^b {f(x) dx} \tag{1}$$を証明せよ。
■ 証明
\(\frac{b-a}{n} = h\) とすると、(1)の左辺は
$$\lim_{h \to 0} {h \sum_{k=0}^{\frac{b-a}{h}-1}{f(a+kh)}} \tag{2}$$と書き換えられる。総和を展開すると
$$\lim_{h \to 0} {h \left( f(a) + f(a+h) + f(a+2h) + \\
\cdots +f \left(a + \left( \frac{b-a}{h}-1 \right) h \right) \right) } \tag{3}$$ここで \(f(x)\) の不定積分(原始関数)を \(F(x)\)とすると、
$$f(x) = \lim_{h \to 0} \frac{F(x+h)-F(x)}{h} \tag{4}$$ なので(4)を(3)に代入すると
\begin{eqnarray}
(3)&=&\lim_{h \to 0} {h \left( \frac{F(a+h)-F(a)}{h} + \frac{F(a+2h)-F(a+h)}{h} + \\
\cdots + \frac{F\left(a+\frac{b-a}{h}h\right) – F\left( a + \left( \frac{b-a}{h}-1 \right)h \right)} {h} \right) } \\
&=&\lim_{h \to 0} \left( F\left( a + \frac{b-a}{h}h \right) -F(a) \right) \\
&=& F(b) – F(a) = \int_a^b {f(x) dx }
\end{eqnarray}(証明終わり)
少し気になっているのは、(2) の h と (4) の h を同じにしていることです。
問題などあれば指摘していただけると助かります。
7

