【量子力学】状態と波動関数の違いは？

量子力学の「状態」と「波動関数」の違いを私なりに説明してみます。

「状態」というのは文字通り、「ある状態」を表します。
「波動関数」は、「観測したときに各状態になる確率を並べたもの」です。

■（例1）離散的な状態の重ね合わせ

例えばあるサイコロについて、
・1か２の目が出た状態を $|1,2\rangle$ 、
・３か４か５の目が出た状態を $|3,4,5\rangle$、
・６の目が出た状態を $|6\rangle$
と書くとします。
$|1,2\rangle$ の状態を取る確率は $\frac{2}{6}$、$|3,4,5\rangle$ の状態を取る確率は $\frac{3}{6}$、 $|6\rangle$ の状態を取る確率は $\frac{1}{6}$ です。

この場合、そのサイコロに蓋をしてどの目が出ているかわからない状態 $|\Psi\rangle$ （大文字のプサイ）は、次のように書くことができます。
$$|\Psi\rangle = \sqrt{\frac{2}{6}}|1,2\rangle+ \sqrt{\frac{3}{6}}|3,4,5\rangle+ \sqrt{\frac{1}{6}}|6\rangle \tag{1}$$グラフに描くとこんな感じです。

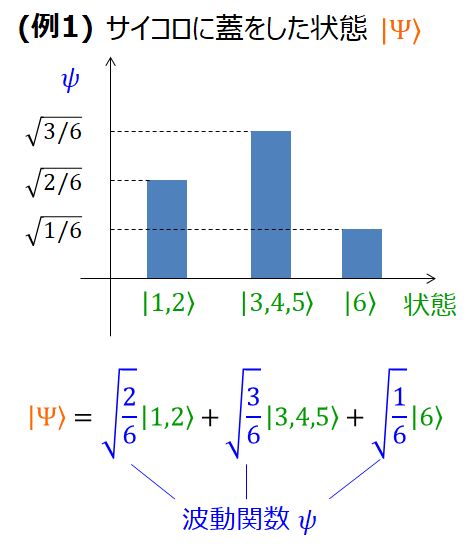各状態の係数 $\sqrt{\frac{2}{6}}, \ \sqrt{\frac{3}{6}}, \ \sqrt{\frac{1}{6}} $ は、2乗するとそれぞれがかかっている状態を観測する確率（$\frac{2}{6},\frac{3}{6}, \frac{1}{6}$）になります。これらの係数 $\left(\sqrt{\frac{2}{6}},\sqrt{\frac{3}{6}}, \sqrt{\frac{1}{6}}\right)$ の組を波動関数と言います。

つまり、このグラフの横軸が状態で、縦軸が波動関数です。

また、 $|1,2\rangle, \ |3,4,5\rangle, \ |6\rangle$ も「状態」ですが、それらの線形和 $|\Psi\rangle$ もまた「状態」です。

■（例2）連続的な状態の重ね合わせ

もう１つ例を挙げましょう。

ある粒子が x 軸上のどこかにいてその座標が不明な場合、その状態 $|\Psi(t)\rangle$ （(1)に相当するもの）はどう表されるでしょうか？

いきなり答えを書いてしまいます。位置 $x$ にいる状態を $|x\rangle$ とすると、
$$|\Psi(t)\rangle = \int_{-\infty}^{\infty} \psi(x,t) |x\rangle dx \tag{2}$$です。$\Psi$ （大文字のプサイ）と $\psi$ （小文字のプサイ）の違いに注意してください。

こちらもグラフに描くとこんな感じです。

(2)は(1)のアナロジーで考えると理解しやすいと思います。
(1)は足し算だったのに対して(2)は積分になっているだけです。
（(2)に $dx$ がつく理由をきちんと説明すると面倒なのでとりあえずここでは「つけないと発散してしまうから」としておきましょう）

このグラフでも横軸$|x\rangle$ が状態で、縦軸 $\psi(t,x)$が波動関数です。
波動関数がようやく波動「関数」らしくなりましたね。こちらの例では、波動関数に時間依存性があることにしました。グラフの波がゆらゆら時間変化するイメージです。

また、(1)と同じく$|\Psi(t)\rangle$ もまた「状態」です。$|\Psi(t)\rangle $ は $t$ にのみ依存します。

■ シュレディンガー方程式は？

シュレディンガー方程式は、$|\Psi(t)\rangle$ について成り立ちます。
$$i \frac{\partial |\Psi(t)\rangle}{\partial t} = \left( – \frac{1}{2m^2} \nabla^2 + V(t,x) \right) |\Psi(t)\rangle \tag{3}$$これに(2)を代入すると
$$\int_{-\infty}^{\infty} \left\{ i \frac{\partial}{\partial t}\psi(t,x) – \left( -\frac{1}{2m^2} \nabla^2 + V(t,x) \right)\psi(t,x) \right\} |x\rangle dx = 0$$異なる $|x\rangle$ が打ち消し合うことはないので、これが成り立つためには { } の中がゼロである必要があります。つまり
$$i \frac{\partial \psi(t,x)}{\partial t} = \left( – \frac{1}{2m^2} \nabla^2 + V(t,x) \right) \psi(t,x) \tag{4}$$状態を含まない、見慣れた「時間を含むシュレディンガー方程式」が得られました。

教科書にはシュレディンガー方程式として(4)がいきなり書かれていることが多いですが、大元は (3) だと考えると整理しやすいと思います。

参考：
・「初級講座弦理論基礎編」p.263あたり

2