区分求積法の証明は高校の教科書に載ってなかった

======(2018.04.15 追記)============
下記の記事の後、区分求積法のオリジナルの高校生にもわかる証明を
こちらの記事
に載せましたので、区分求積法の証明を期待してたどり着いた方は上の「こちらの記事」のリンク先をご覧ください。
=============================




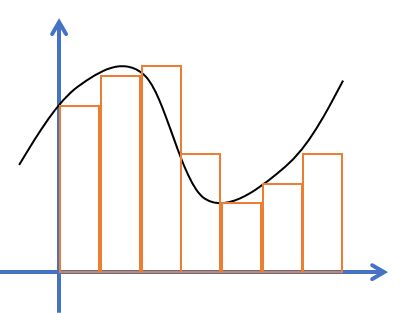
高校数学を学ばれた方なら「区分求積法」はご存知だと思います。

式で書くと
$$\lim_{n\to\infty}{\frac{b-a}{n}\sum_{k=1}^{n} f\left( a+ \frac{k(b-a)}{n} \right) }=\int_{a}^{b}f(x)dx$$というやつです。

大学入試問題では普通に使う式ですが、実はこの式、高校の教科書には証明が載ってないんですね。知らなかった。

\( f(x) \) が \( a \leq x \leq b \) で単調増加関数か単調減少関数なら比較的簡単に証明できます（例えば こんな感じ）。いわゆる「はさみうちの原理」ですね。でも増加と減少の両方を含む関数だと少し工夫が必要そうです。


ネットを探してみたところ、こんな証明がありました。
区分級数はりーマン和の特別な場合なんですね。

これなら高校生でも理解できそうな気もするなーと思いながら検索を進めると、「一昔前はりーマン和が定積分の定義として教科書に載っていた」という記事を見つけました（参考サイト）。

そうだったのか。。


参考：
・ワナにはまらない微分積分 (メダカカレッジ)