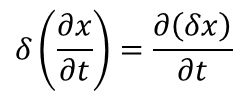各種直交座標系での勾配(gra…
波動方程式を弦の振動から導出する場合の補足

偏微分方程式の教科書で、波動方程式をギターやバイオリンのような弦の振動を使って導出しているのをよく見ます。だいたい次のような図とセットになっています。
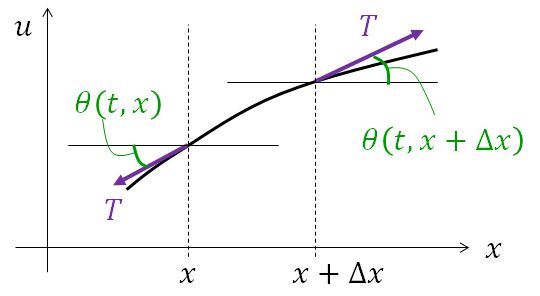
この図のような弦の振動から波動方程式
$$\frac{\rho}{T} \frac{\partial ^2 u}{\partial t^2} = \frac{\partial ^2 u}{\partial x^2} \tag{1}$$を導出しようとすると、下記①~⑤の仮定が必要になります。
<仮定>
① 弦の運動は、その静止時の位置(以下 x 軸とする)を含む、ある平面内に限られる
② 弦の各部分はほぼ x 軸と垂直な方向にのみ動く(横波)とする
③ 弦は一様な線密度 \(\rho\) を持つ
④ 張力 \(T\) は運動の間どこも一定で、かつ弦の接戦方向に働くとする
⑤ 弦と x 軸とが成す角は微小に保たれる
これら①~⑤が満たされるなら、弦の素片の u 方向の運動方程式として(1)の波動方程式が得られるというわけです。
でもちょっと待ってください。
例えば仮定⑤では微小振動を仮定しています。ということは微小ではない弦の振動は波動方程式では表せないのでしょうか?

実はそのとおり、表せないんです。
微小振動ではない場合も考慮した弦の振動を表す微分方程式は次のようになります(記事最後の参考文献参照)。
$$\rho \frac{\partial^2 u}{\partial t^2} = \frac{\partial}{\partial x}\left( \frac{T \frac{\partial u}{\partial x}}{\sqrt{1 + \left( \frac{\partial u}{\partial x} \right)^2}} \right)$$
こう書くと「波動方程式って、微小振動しか表せないならたいした応用ができないのでは?」と思われるかもしれません。
しかしそうじゃないんです。逆なんです。
どういうことかというと、
「まず、もっと忠実に(1)の波動方程式に従う物理現象がある。
弦の振動がそれと同じ方程式を満たすためには、微小振動を仮定する必要がある。」
ということです。
「もっと忠実に波動方程式に従う物理現象」とは何か? 例えば電磁波です。
電磁波は空間自体が振動するわけではなくて電場や磁場が電磁波の進行方向と垂直な方向に振動します。
電場や磁場の挙動を表すのはマクスウェル方程式です。マクスウェル方程式を変形することで、仮定や近似を使わずに、電場と磁場それぞれについて波動方程式を導くことができます。過程は割愛しますが結論として次のような波動方程式が得られます。
$$\epsilon \mu \frac{\partial ^2 \vec{E}}{\partial t^2} = \nabla ^2 \vec{E} \\
\epsilon \mu \frac{\partial ^2 \vec{H}}{\partial t^2} = \nabla ^2 \vec{H}$$
弦の場合に微小振動を仮定する必要がある理由は、微小振動でないと、弦の素片は縦方向と横方向の両方に無視できない力を受けるからです。
とはいえ波動方程式の導出に弦の振動を用いると、弦の素片についての運動方程式 \(m\vec{a}=\vec{F}\) からシンプルに導出できるというメリットがあります。波動方程式の導出のためにマクスウェル方程式を持ち出すのは、電磁気学を未習の人も読む可能性を考えるとやめておいた方がいいかもしれません。
ただ「波動方程式って微小振動にしか使えないの?」という誤解を生まないために補足してみました。
参考:
偏微分方程式入門 (基礎数学)

0