微分と変分は順序を交換できる

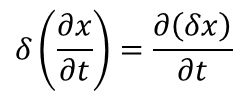
最小作用の原理を使って作用から運動方程式を立てるときに、よく
$$\delta \left( \frac{\partial x}{\partial t} \right) = \frac{\partial (\delta x)}{\partial t}$$という関係式を使います。「微分と変分の順序を交換できる」というわけです。

このことを使っている本はよく見ますが、そう変形していい理由はあまり見ないので書いておきます。といっても大したことではないのですが。
$$\delta \left( \frac{\partial x}{\partial t} \right)
= \frac{\partial (x + \delta x)}{\partial t}-\frac{\partial x}{\partial t}
= \frac{\partial (x + \delta x – x)}{\partial t}
= \frac{\partial (\delta x)}{\partial t}$$
これだけです。