ポテンシャルから波動関数の形を簡易的に予想する方法

（一番下に参考文献を載せてあります）

井戸型ポテンシャルに代表されるように。

量子力学では、与えられたポテンシャルエネルギーの空間分布 $V(x)$ に対して、波動関数 $\psi(x)$ がどのように分布するかを計算してからエネルギーや期待値などを求めることが多いと思います。

よくある解き方の流れはこんな感じだと思います。
=====
(1) シュレディンガー方程式に $V(x)$ を代入して$\psi(x)$ について解く
　　↓
(2) 境界条件から未定の係数やエネルギーを求める
　　↓
(3) 得られた波動関数$\psi(x)$ を規格化する
　　↓
(4) 規格化した波動関数$\psi(x)$ から存在確率分布、期待値などを求める
=====

本記事では、(1)をやる前に波動関数 $\psi(x)$ のおよその形を予想する方法をご紹介します。

結論を先に書くと、こうなります。

・$E \gt V(x)$ の領域・・・$\psi$ は定常的
・$E \lt V(x)$ の領域・・・$\psi$ は指数関数的で、$x\to\pm \infty$ でゼロに収束する

例えばポテンシャルと粒子のエネルギーの関係が下図左側のような場合、波動関数は下図右側のようになることが予想できます。

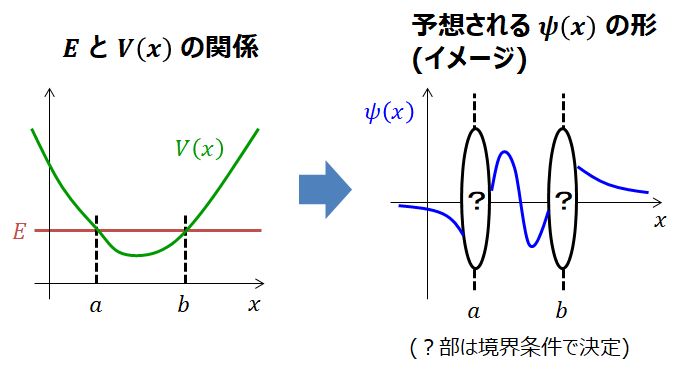
以下にその理由を説明します。

まず、時間に依存しないシュレディンガー方程式
$$\left(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V(x)\right)\psi(x)=E\psi(x)$$を次のように変形します。
$$\frac{d^2\psi(x)}{dx^2}=-\frac{2m}{\hbar^2}(E-V(x))\psi(x)$$この微分方程式の解は、$E-V(x)$ の符号によって形が異なります。

(1) $E-V(x)>0$ の領域では
解は $\psi(x) = A \cos(kx) + B \sin(kx)$ の形になります。
これは係数が複素数ですが三角関数の和ですので定常的なイメージです。

(2) $E-V(x)<0$ の領域では
解は $\psi(x) = C e^{kx} + D e^{-kx}$ の形になります。
こちらも係数は複素数ですがexp関数ですので、数学的には $x \to \pm \infty$ で0または無限大のイメージです。
しかし $\psi$ が物理的には波動関数であることを考えると、 $x \to \pm \infty$ で発散する解は不適です（例えば規格化できないという問題が出てきます）。
そのため「$x \to \pm \infty$ でゼロに収束する」という条件が必要になります。

また以上の考え方を適用すると、例えば波動関数が無限遠方まで広がるような状態を実現するには、$x \to \pm \infty$ で $E \gt V(x)$ である必要があることがわかります。

参考：
シュレディンガー方程式 ―基礎からの量子力学攻略― (フロー式物理演習シリーズ 19)