変分原理の概要図

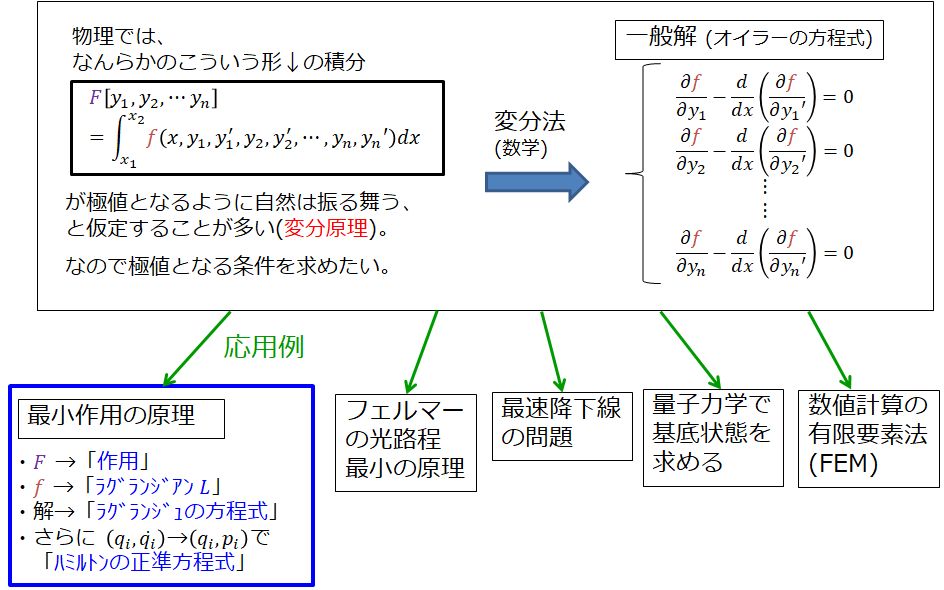
勉強会やセミナーで使っている、変分原理の概要をまとめた図をご紹介します。

こちらです↓簡単に説明します。

物理では、
$$F(y_1,y_2,\cdots,y_n)=\int_{x_1}^{x_2}f(x,y_1,y_1′,y_2,y_2’\cdots,y_n,y_n’)dx$$という形の関数 \(F\) が極値をとるように自然は振る舞う、と仮定することが多いです。

これを「変分原理」と言います。

そのため、関数 \(F\) の極値を求めたくなります。

ありがたいことに、この極値を求める問題は数学的に一般解（オイラーの方程式）が得られています。こちらです。
\begin{eqnarray}
\left\{
\begin{array}{c}
\frac{\partial f}{\partial y_1} – \frac{d}{dt}\left( \frac{\partial f}{\partial y_1′} \right) =0 \\
\frac{\partial f}{\partial y_2} – \frac{d}{dt}\left( \frac{\partial f}{\partial y_2′} \right) =0 \\
\vdots \\
\frac{\partial f}{\partial y_n} – \frac{d}{dt}\left( \frac{\partial f}{\partial y_n’} \right) =0
\end{array}
\right.
\end{eqnarray}「解」と書いておきながら方程式がたくさん並んでいる理由は、 \(F\) が関数 \( y_1,y_2,\cdots,y_n \) の関数だからです（関数の関数のことを汎関数といいます）。


このことの応用例して、
・最小作用の原理
・フェルマーの光路程最小の原理
・最速降下線の問題の解法
・量子力学で基底状態を求める手法
・数値計算の有限要素法（FEM）
などがあります。

例えば最小作用の原理では、変分法を下記のようにあてはめることで運動方程式を得ることができます。
・\(F\) →　作用S
・\(f\) → ラグランジアンL
・\(y_n\) → 粒子の位置 \(q\)
・\(y_n’\) → 粒子の速度 \(\dot{q}\)
・解 → ラグランジュの運動方程式
（ラグランジュの運動方程式は、\((q_i,\dot{q}_i)\)を\((q_i,p_i)\)に置き換えるとハミルトンの正準方程式になります）