[相対論] 加速系への座標変換を図で表すと？

【動機】加速系への座標変換の話はどこへ行った？

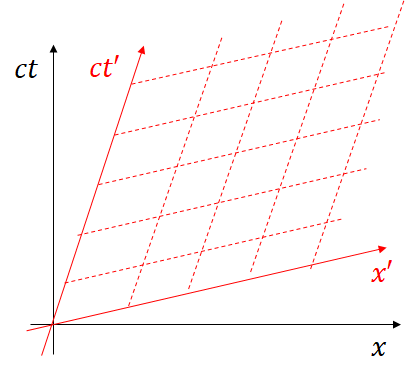
特殊相対論では、ある慣性系 S に対して等速で動く慣性系 S’ を考えました。
このとき S から見た S’ 系の座標軸が、下記のようにひし形にひしゃげて見えることはいろんな本に書かれていると思います。


一般相対論の初学者である私は、このあと一般相対論に入るときに「次は加速系への変換方法の話になるのかな」と予想（期待）していました。

しかし実際読み進めると、多くの本では加速系の話ではなく曲線座標やら重力やらの話が出てきて、「加速系への座標変換はどうなった？？」というモヤモヤを抱えたまま読み進めることになりました。

ガリレイ変換でもそこそこイメージできる

そんな中、この本は違いました。

加速する系 S” の速度が光速と比較して十分小さければガリレイ変換で近似できます。
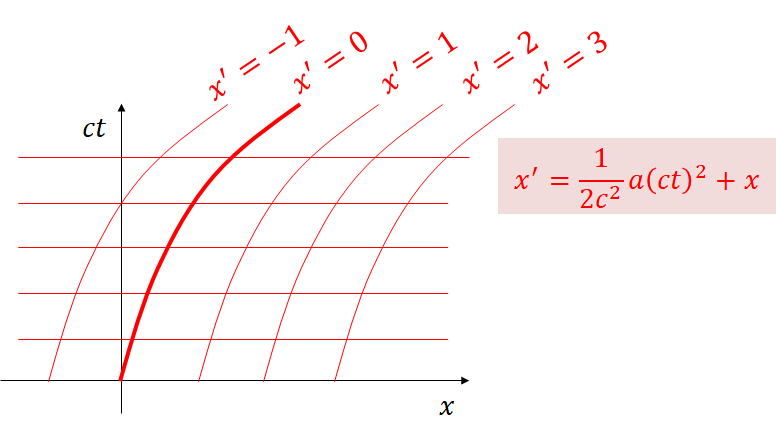
ベースとなる慣性系 S での座標を \(x\)、S に対して加速度 \(a\) で加速する系 S” での位置を \(x’\) 、時刻 \(t=0\) を S と S” で共通とすると変換式は下記のようになります。
$$x’ = \frac{1}{2} a t^2 + x = \frac{1}{2c^2} a (ct)^2 + x$$図示するとこんな感じ。（これもミンコフスキー図って呼ぶのかは不明）
二次曲線です。
一定の速度だと（ひし形の）直線だったのが、加速することで立派に曲がってますね。

このように、相対論の効果を考慮しなくても、ガリレイ変換を使えば S” の座標軸が S からどのように見えるのかイメージが湧きます。

一般相対論を考慮すると？

さきほどのグラフでは、加速すると曲がることはわかったものの、速度が無限に大きくなる（＝グラフの傾きが限りなく0に近づくことができる）という問題を抱えています。

一般相対論を考慮するとそのあたりが補正できます。

一般相対論の効果を考慮した加速系の座標をリンドラー座標 (Wikipedia) というそうです。
座標軸を図示するとこんな感じ。

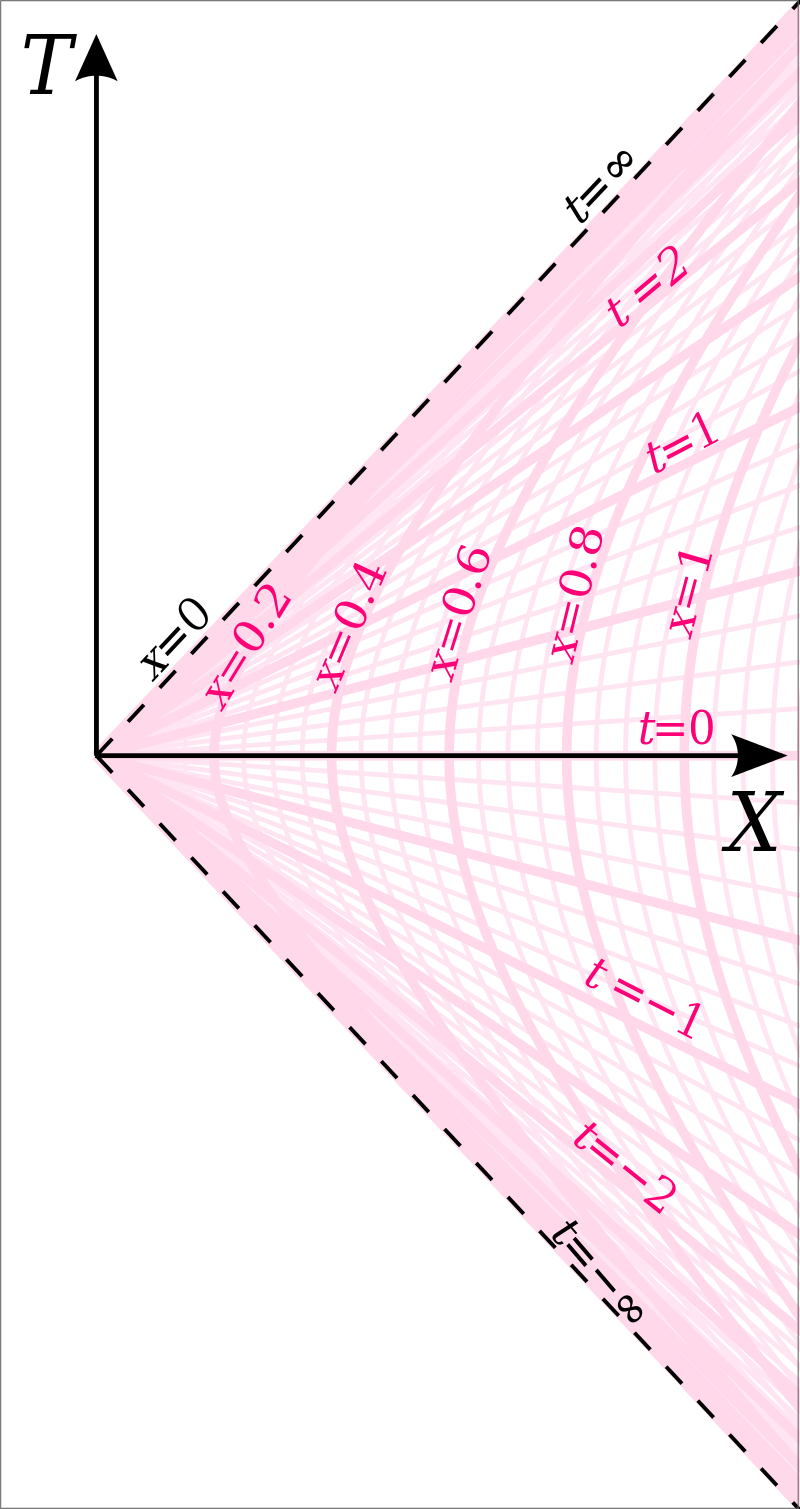
（図は Wikipedia からコピーしたもので、x が X に、x’ が x に、ct が T に置き換わってます。）

x’=一定 （図の x = 一定）の軌跡の接線を見ると、ちょうどガリレイ変換の図に対して光速の漸近線を設けた感じですね。
どの点をとっても光速を超えない（傾きが1より小さくならない）様子がわかります。

（おまけ）実はローレンツ変換しなくてもひしゃげる

となるとこんな期待も出てきます。

特殊相対論のひし形の座標系への変換も、ローレンツ変換を出すまでもなく、ガリレイ変換で近いものが得られるのでは？

はい、実際これもできますね。
変換式は次のとおりです。
$$x’ = V t + x = \frac{V}{c} (ct) + x$$図示するとこんな感じになります。

V が c と比較して十分小さいときは、x’ = 一定 の直線が ct 軸にほぼ平行になり、元の座標系とほとんど変わらないことがわかります。