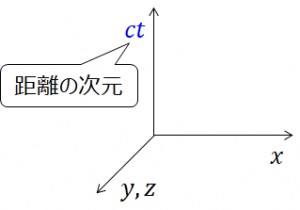
ベクトルの反変成分、共変成分、…
【相対論】自分が立っている地面が曲がっているかを確認する方法

曲がりには 2 種類ある
一般相対論で考慮する曲がりには下記2つの種類があります。(1) 空間そのものが曲がっているタイプ
(2) (空間そのものは曲がってなくても)空間に設定した座標軸が曲がっているタイプ
(2) は相対的なものです。ある座標系から見れば曲がっているように見える座標系も、別の座標系から見れば曲がってない可能性があります。
こちらの(2)のタイプについてはこの記事ではこれ以上触れません。
一方 (1) のタイプについては、自分は最初下記のように思っていました。
空間の曲がりも相対的なのでは?
例えば地球の表面は丸いけど、メルカトル図法で紙に描けば平坦になるし。
しかし下記の書籍を読んで、たしかに空間や平面自体の曲がり具合を測定できると納得できたので紹介します。
・ブラックホールと時空の方程式:15歳からの一般相対論
2つの方法に共通する舞台設定として、地球の表面からは離れられない状態(可動範囲が2次元)で、自分の立っている地面ががたしかに曲がっていることを確認しようとしているとします。
【方法1】ベクトルの矢印オブジェを抱えたまま、向きを変えずにある領域をぐるっと1周する方法
1つめの方法は、まず、ベクトルの矢印を表すオブジェを1つ用意します。で、そのオブジェを抱えたまま、オブジェの向きを変えずにある領域をぐるっと1周するんです。
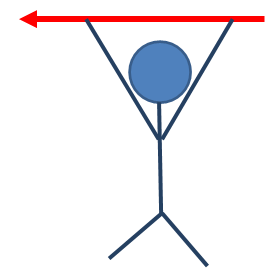 もしも元の位置に戻ってきたときにオブジェの向きが出発したときと比べてズレていたら、その通った経路は2次元平面内に収まってなかったということがわかります。
もしも元の位置に戻ってきたときにオブジェの向きが出発したときと比べてズレていたら、その通った経路は2次元平面内に収まってなかったということがわかります。具体例でみてみましょう。
例えば、下記のように進むところを想像してみてください。
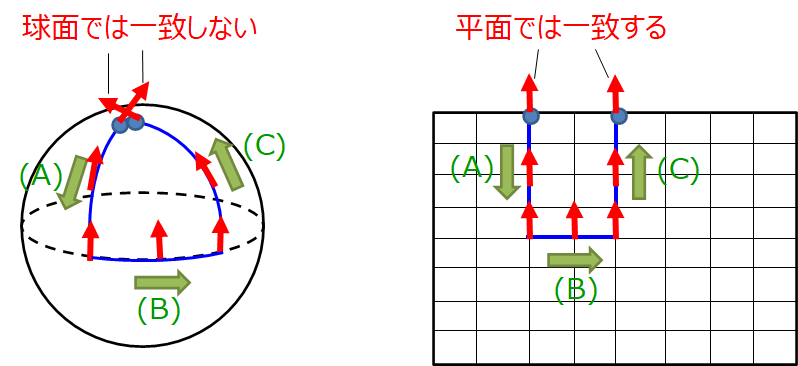
(A) 北極点をスタートして、東経0度の経線に沿って赤道まで進みます。その際、矢印のオブジェを、常に北の方角を指した状態を維持して抱えながら進みます。
(つまり、常に進行方向と逆方向に矢印を向けたまま進みます。)
(B) さらに、矢印は北の方角を向けたまま、赤道に沿って東経45度の位置まで進みます。
(C) 東経90度の経線に沿って北上して北極点に戻ってゴールです。
(常に進行方向と同じ方向に矢印を向けたまま進みます。)
上記 (A) → (B) → (C) のように進んだ場合に、もしも地球の表面が平らであれば、ゴールした時の矢印は最初と同じ向きです(2次元のメルカトル図法の地図を想定してもらえるとわかると思います)。しかし実際の地球の表面は曲がってますので、戻った時の矢印の向きは90度ズレているはずです。
(本当はもっと小さな領域でいいのですが、わかりやすくするため赤道まで降りました。)
これにより、地球の表面から離れられない人でも、地球の表面が曲がっていると判断することができます。
【方法2】 円を描く方法
もう1つ方法があります。
地表に、ある点を中心とした半径 \( r \) の円を描く方法です。
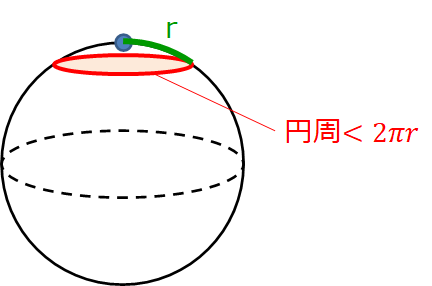
もしも地表が平らであれば円周の長さは \(2 \pi r\) です。
一方、もしも図のように凹凸があると半径はその凹凸に沿った曲線になりますので、円周の長さは \( 2 \pi r \) よりも短くなります。
こちらの方法でも、同じことが確認できます。
【方法1】も【方法2】も座標系に依存した操作は不要なので、座標系によらず地表が曲がっていることが確認できたことになります。
0