「A ならば B である」 の A と B の包含関係の覚え方

数学で「A ならば B である」という形の文章をよく目にします。
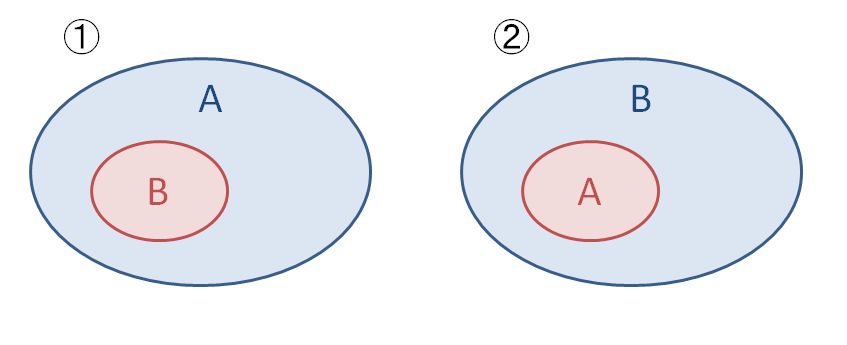
このとき、AとBの包含関係はベン図で書くと下図①② のどちらでしょうか？
私は、高校時代の数学の先生に教えてもらった覚え方でいまだに覚えています。

それは、「人間ならば動物である」を例に考えることです。

この場合ですと、A が人間で B が動物です。
そうすると明らかに包含関係は上図の②が正解であることがわかります。



■ おまけ：　必要条件か？十分条件か？

ちなみに 「AならばBである」を「A → B」と書いたりします。
A → B のとき、A はB であるための必要条件でしょうか？十分条件でしょうか？

これも私には覚え方があります。

それは　A → B の順に 「十分必要」 と覚えておくことです。
すると、
・A は B であるための十分条件、
・B は A であるための必要条件
であることがわかります。

「人間である」ことは「動物である」ための十分条件ですし（人間であれば必ず動物）、
「動物である」ことは「人間である」ための必要条件であることとも一致しています。