総乗記号は途中で分割できる

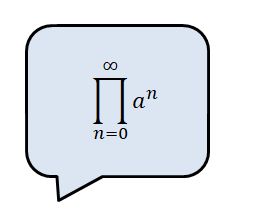
高校で習う総和（シグマ）記号はこんな意味でした。
$$\sum_{n=0}^{\infty}a^n = a^0 + a^1 + a^2 + \cdots$$大学では、これに似た記号として総乗（パイ）という記号が出てきます。
$$\prod_{n=0}^{\infty}a^n = a^0 a^1 a^2 \cdots$$総和が足し算なのに対して総乗は掛け算になっています。ただそれだけです。

総乗記号の性質として、「途中で分割できる」というのがあります。
どういうことかというと、例えば
$$\prod_{n=0}^{\infty}\left( a^n n \sin{n} \right)
=\prod_{n=0}^{\infty}a^n \prod_{n=0}^{\infty}n \prod_{n=0}^{\infty}\sin{n}
=\prod_{n=0}^{\infty}a^n \prod_{n=0}^{\infty}\left( n \sin{n} \right) $$ のようにできるということです。総和の意味を考えればそうなりますよね。