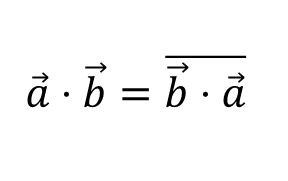行列どうしの内積

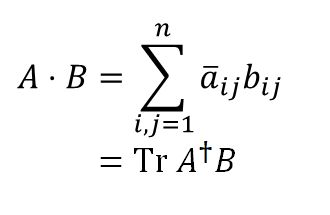
ベクトルどうしに内積が定義できるのと同じように、行列どうしの間にも内積を定義することができます。

このとき、例えば 2×2複素行列でしたら、4次元の複素ベクトル空間を作ることになります。

■ 行列どうしの内積の定義式

行列どうしの内積は、成分を複素数とすると次のように定義されています。

$$A \cdot B = \sum_{i,j=1}^{n} \bar{a}_{ij} b_{ij} \tag{1}$$

複素ベクトルの内積の定義
$$\vec{a} \cdot \vec{b} = \bar{a}_1 b_1 + \bar{a}_2 b_2 + \cdot + \bar{a}_n b_n$$の自然な拡張になっていますね。

■ 行列の内積は対角和（トレース）を使っても計算できる

(1)は、次のようにトレースを使って計算することもできます。

$$A \cdot B = \mathrm{ Tr } \ (A^\dagger B)$$

「行列のトレースって何に使うんだろう？」と疑問だった方！こんなところに使えるんです。
（証明は参考資料のp.54参照）

■ 行列の内積はベクトルの内積と同じ性質を持つ

行列の内積は、下記のようにベクトルの内積と同じ性質を持ちます。
(i) $A \cdot B = \overline{B \cdot A}$
(ii) $(A+B) \cdot C = A \cdot C + B \cdot C$
(iii) $\alpha A \cdot B = \bar{\alpha} A \cdot B, \ \ A \cdot \alpha B = \alpha A \cdot B $
(iv) $A \cdot A \ge 0$
(v) $A \cdot A = 0$ ならば $A = 0$
（証明は参考資料のp.54参照）

(iii) では $\alpha$ がどちらにかかっているかでくくりだし方が変わることに注意してください。

■ 正規直交基底の定義

内積が定義できるなら、ベクトルと同様に行列にも正規直交基底が定義できます。

例えば2×2行列の正規直交基底の一例としては、
$$\vec{e}_{11} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \vec{e}_{12} = \begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix}, \vec{e}_{21} = \begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}, \vec{e}_{22} = \begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix}$$があります。

たしかに各行列はノルムが1で直交していることが確認できます。

また、任意の行列は
\begin{eqnarray}A&=&\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \\
&=& a_{11} \vec{e}_{11} + a_{12} \vec{e}_{12} + a_{21} \vec{e}_{21} + a_{22} \vec{e}_{22}
\end{eqnarray}という具体に正規直交基底の線形和に分解することができます。

参考：
キーポイント行列と変換群 (理工系数学のキーポイント (8))