【ZERO】「情報科学の名探偵！?魔法の数式スパースモデリング」まとめ

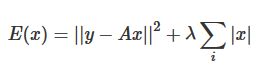
下記番組のまとめを書きます。

放送局	NHK
番組名	サイエンスZERO（サイエンスゼロ）「情報科学の名探偵！?魔法の数式スパースモデリング」
放送日時	2015年8月23日

目的は、「見逃してしまった人に、概要だけでもお伝えすること」です。

この番組は今でも「U-NEXT」というサイトでオンデマンドで視聴できる可能性があります（タイミングによります）。

「サイエンスZERO」のタイトル一覧はこちらです。

導入部より引用

突然ですが名探偵に共通する能力といえばいったい何を思い浮かべますか？

推理力？洞察力？限られた情報の中から総合的に考える？

そう、そんな名探偵が今、科学の世界で大活躍してるんです。
医療の現場では、MRIにかかる時間が大幅に短縮。地質の研究では津波が押し寄せてきた地層を高い確率で分析。

そう、名探偵の正体とは、この数式。
$$E(x) = {||y-Ax||}^2 + \lambda \sum_i |x|$$その名もスパースモデリング。

これを使えばなんとブラックホールの正体にも迫れると期待されています。

データを読み解きものごとの本質にたどりつく科学界の名探偵スパースモデリング。
その驚きの能力に迫ります！

要点

スパースモデリングの数式１つで、少ない情報と全体を結びつけることができる。
主な応用方法は下記の２つ。
① 少ない情報から残りの情報を精度よく予測する
② ビッグデータから重要なデータを探す

詳細

スパースモデリング・・・少ない情報で正解にたどり着く数学的手法。

数式は
$$E(x) = {||y-Ax||}^2 + \lambda \sum_i |x|$$・左辺の $x$ が「求めたい答え」。
・右辺第1項の ${||y-Ax||}^2 $ は答えの候補を選ぶ役割。
　・$y$ は「観測データ」、$Ax$ は「答えの候補」。
・右辺第2項の $\lambda \sum_i |x|$ は答えの候補を絞る役割。

数式のキモは、
・解の候補を出すことと、そこから解を絞ること
・それを繰り返しながら両方の条件（命令）をうまくバランスさせることが重要

■ 少ない情報から残りの情報を精度よく予測する

応用1: 医療
脳のMRIが、通常9分かかるところがスパースモデリングを使うと3分弱で終わる。

応用2: 宇宙
・ブラックホールの可視化に役立ちそう
・ブラックホールの周囲のガスが飲み込まれる直前に放つ光を観測して、ブラックホールの形を可視化するプロジェクト。
その際、世界数か所にある望遠鏡のデータを集めてもデータが足りない部分がある。そこをスパースモデリングで補完する。

他にも50以上のプロジェクトで応用中。

■ ビッグデータから重要なデータを探す

・津波の堆積物の化学組成の割り出し
　・18個の元素を指標の候補にしていたが、スパースモデリングによって7個棄てて11個の方が精度が向上することがわかった。

・人の顔を見分けられない脳の障害の研究
脳の神経細胞というビッグデータから、人の顔を認識する機能に関するものを選び出すのに使える。